Perai!

é indeterminado porque não sabemos quais foram as formulas que geraram estes infinitos.
O mesmo serve para os outros casos.
digamos que tenhamos um infinito gerado por esta formula:
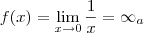
que não é o mesmo que este(que também é infinito):
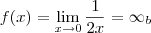
Apesar de termos um

e um

ambos são diferentes.
Se fossem iguais, a divisão teria resultado 1.
No caso acima,
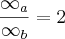
A indeterminação só surge quando não conhecemos as formulas que geraram os infinitos e os zeros.
Lembremos que não existe valores fisicos no universo que representem infinito ou o zero. São abstrações e por isso nos obriga a manter suas formulas de origem para que possamos resolver as "indeterminações".
O mesmo vale para o

porque se este 1 da formula for

então:
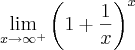
tem resultado 'e' (2,7...)
Eu acredito que padrões de eventos do mundo foram descobertos e relacionados com os códigos(que inventamos). Para cada evento novo que era descoberto e que não era composto pelos signos que já conheciamos ganhava uma descrição nova, um simbolo novo e uma forma de se usá-lo. O cálculo simbólico (Matemática simbólica) foi inventado para se assemelhar aos eventos reais. Seus resultados (previsões) são traduzidos para o real com grande perfeição. Poderiamos inventar outras matemáticas, sem conexão com eventos ou fatos reais, mas isso dependeria de que o inventor dessa nova matemática descrevesse como esse mundo novo funciona. A Matemática (cálculo simbólico) foi inspirada nos eventos reais.
Os planetas continuariam orbitando os sois se mudassemos o 2 que eleva a distância por outro valor > 2:

Acretido que a matemática seja exata e humana.
A parte humana da matemática é apartir da lógica fuzzy, onde armor, ódio, bonito, feio, se torna mensurável.
Não sei se estou certo, mas acho que lógica

Matemática.









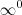

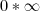

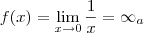
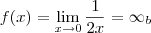
 e um
e um  ambos são diferentes.
ambos são diferentes. 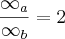
 então:
então: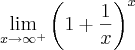 tem resultado 'e' (2,7...)
tem resultado 'e' (2,7...)
 Matemática.
Matemática.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)