A função diferenciável y = f(x) é tal que para todo x?D(f) , o ponto (x, f (x) ) é solução da equação
xy³ + 2xy² + x = 4 . Calcule a equação da reta tangente ao gráfico de f no ponto (1, f (1) ).
por rodrigo lara » Sex Dez 27, 2013 20:31
por e8group » Sex Dez 27, 2013 22:10
é dada implicitamente pela equação (dada) e temos (por simplicidade omitiremos a dependência de f por x )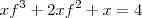 
.Derivando-se ambos lados com respeito a 
(Atenção as regras : Cadeia ,produto) ,segue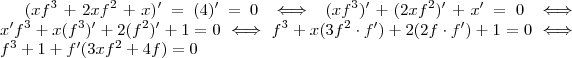 
. ![[f(x)]^3 + 1 + f'(x) (3x[f(x)]^2 +4f(x)) = 0](/latexrender/pictures/3f6c96553bc72f9a2f09f2ccf6f24db1.png "[f(x)]^3 + 1 + f'(x) (3x[f(x)]^2 +4f(x)) = 0")
que substituindo o ponto dado dos dá ![[f(1)]^3 + 1 + f'(1) (3[f(1)]^2 +4f(1)) = 0](/latexrender/pictures/0b6fd717b5d70621acef11587d25ad29.png "[f(1)]^3 + 1 + f'(1) (3[f(1)]^2 +4f(1)) = 0")
(*) 
,substituindo o ponto dado na eq.dada ,ficando com ![[f(1)]^3 +2[f(1)]^2 +1 = 4 \iff [f(1)]^3 + 2[f(1)]^2 - 3 = 0](/latexrender/pictures/412f08fe859c4181013ec33399f8fd8d.png "[f(1)]^3 +2[f(1)]^2 +1 = 4 \iff [f(1)]^3 + 2[f(1)]^2 - 3 = 0")
e podemos ver que no ponto 
trata-se uma raiz da eq. polinomial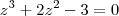 
que és apenas 1 . Aqui determinamos 
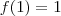, substituindo este resultado em 
será possível determinar 
e por conseguinte a eq. da reta tangente ao gráfico de no ponto estará bem definida que és 
. 
por rodrigo lara » Ter Jan 07, 2014 21:28
por e8group » Ter Jan 07, 2014 22:21
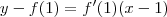Voltar para Cálculo: Limites, Derivadas e Integrais
por Sobreira » Dom Dez 08, 2013 14:27
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a e elevar ao quadrado os dois lados)