(
 ) "
) "Por favor, não quero a resolução e nem mesmo decorar fórmulas. Quero entender a questão. Quando tentei resolver, deu errado. Por favor, ajudem....
Obrigada!

 ) "
) "
 e
e  . Considere
. Considere 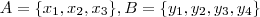 e seja
e seja  o conjunto das aplicações
o conjunto das aplicações injetoras .Notando que
injetoras .Notando que 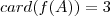 ,poderíamos pensar em quantos subconjuntos (distintos) de
,poderíamos pensar em quantos subconjuntos (distintos) de  possui cardinalidade 3 . Nota :
possui cardinalidade 3 . Nota : 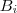 de B com 3 elementos é possível obter o mesmo número de aplicações injetivas tais que
de B com 3 elementos é possível obter o mesmo número de aplicações injetivas tais que 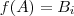 .
.  cuja o conjunto imagem é
cuja o conjunto imagem é  , o que difere cada aplicação é a regra de associação . E a cada par de aplicações cujos conjuntos imagens são respect.
, o que difere cada aplicação é a regra de associação . E a cada par de aplicações cujos conjuntos imagens são respect. 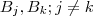 o que difere estas funções são os conjuntos imagens .
o que difere estas funções são os conjuntos imagens . 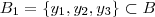 . É possível definir
. É possível definir  aplicações injetivas (distintas) . Ora , se
aplicações injetivas (distintas) . Ora , se 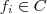 podemos ter
podemos ter 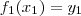 ou
ou  ou ainda
ou ainda  .Assim , basta por
.Assim , basta por  (j=1,2,3) .
(j=1,2,3) . 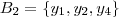
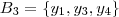
 .
. ).
). injetivas (distintas) , em linguagem de conjunto
injetivas (distintas) , em linguagem de conjunto 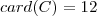 .
. 

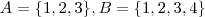 . E defina
. E defina  injetora . Segue-se que
injetora . Segue-se que  pode tomar 4 valores ,
pode tomar 4 valores , 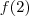 pode tomar 3 valores e
pode tomar 3 valores e 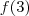 2 valores . Assim o número total de funções injetivas é
2 valores . Assim o número total de funções injetivas é  .
.  injetora .
injetora . 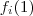 pode tomar 4 valores ,suponha
pode tomar 4 valores ,suponha 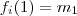 .Então
.Então  pode tomar um dos 4 valores exceto m ,suponha
pode tomar um dos 4 valores exceto m ,suponha  e
e  pode tomar um dos 4 valores exceto
pode tomar um dos 4 valores exceto  , suponha
, suponha 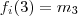 . Estas palavras acima se resume em :
. Estas palavras acima se resume em :  .
.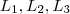 .Marque 4 pontos sobre L_1 , 3 pontos sobre a reta L_2 e 2 sobre a L_3 (em que estes pontos podem ser visto com os valores que m_i podem assumir ,escolhendo um na primeira reta ,na segunda reta terá 3 possibilidades todas distintas da escolha anterior e assim por diante )
.Marque 4 pontos sobre L_1 , 3 pontos sobre a reta L_2 e 2 sobre a L_3 (em que estes pontos podem ser visto com os valores que m_i podem assumir ,escolhendo um na primeira reta ,na segunda reta terá 3 possibilidades todas distintas da escolha anterior e assim por diante ) e escolhendo um caminho dentre os
e escolhendo um caminho dentre os  que há para chegar em um dos pontos de
que há para chegar em um dos pontos de  .Chegando lá , podemos escolher um caminho p/ chegar em um dos pontos de
.Chegando lá , podemos escolher um caminho p/ chegar em um dos pontos de 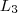 dentre os 3 disponíveis . Para cada procedimento completo nos fornecerá uma aplicação injetiva .Só aqui já conseguimos ,
dentre os 3 disponíveis . Para cada procedimento completo nos fornecerá uma aplicação injetiva .Só aqui já conseguimos ,  aplicações injetoras .
aplicações injetoras .  e fazendo o mesmo acima obteremos
e fazendo o mesmo acima obteremos  aplicações injetoras e assim por diante podemos obter no total
aplicações injetoras e assim por diante podemos obter no total  aplicações injetoras .
aplicações injetoras .




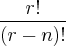 .
.



Voltar para Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.