 por Pessoa Estranha » Ter Dez 17, 2013 22:35
por Pessoa Estranha » Ter Dez 17, 2013 22:35
"SE A E B SÃO CONJUNTOS E A
QUANTIDADE DE ELEMENTOS EM A É n E A
EM B É r, QUANTAS FUNÇÕES f : A ----> B, INJETORAS EXISTEM ?
(

) "
Por favor, não quero a resolução e nem mesmo decorar fórmulas. Quero entender a questão. Quando tentei resolver, deu errado. Por favor, ajudem....
Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Qua Dez 18, 2013 17:59
por e8group » Qua Dez 18, 2013 17:59
Veja um exemplo para

e

. Considere
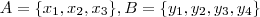
e seja

o conjunto das aplicações

injetoras .Notando que
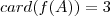
,poderíamos pensar em quantos subconjuntos (distintos) de

possui cardinalidade 3 . Nota :
Para cada subconjunto
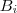
de B com 3 elementos é possível obter o mesmo número de aplicações injetivas tais que
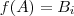
.
Obs.:
Em relação as apliçaões

cuja o conjunto imagem é

, o que difere cada aplicação é a regra de associação . E a cada par de aplicações cujos conjuntos imagens são respect.
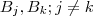
o que difere estas funções são os conjuntos imagens .
Exemplo :
Seja
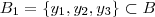
. É possível definir

aplicações injetivas (distintas) . Ora , se
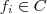
podemos ter
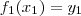
ou

ou ainda

.Assim , basta por

(j=1,2,3) .
Mas ainda há outros subconjuntos de B ,
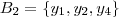
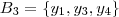

.
(Note que o número de subconjuntos com cardinalidade = 3 pode ser calculado por

).
Logo , ao todo é possível definir 12 aplicações

injetivas (distintas) , em linguagem de conjunto
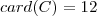
.
O que acha ? Caso esteja correto ,dá para generalizar utilizando o raciocínio acima ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por tenebroso » Qua Dez 18, 2013 18:34
por tenebroso » Qua Dez 18, 2013 18:34
ALGUÉM PODERIA DAR UMA AJUDINHA LÁ EM MINHAS QUESTÕES...? EHHEHEHEHE..

-
tenebroso
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Dez 18, 2013 16:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: estudante
- Andamento: cursando
 por e8group » Qua Dez 18, 2013 20:51
por e8group » Qua Dez 18, 2013 20:51
Não está certo .
Por exemplo ,considere
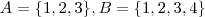
. E defina

injetora . Segue-se que

pode tomar 4 valores ,
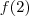
pode tomar 3 valores e
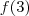
2 valores . Assim o número total de funções injetivas é

.
Justificativa .
Defina

injetora .
Como vimos
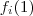
pode tomar 4 valores ,suponha
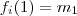
.Então

pode tomar um dos 4 valores exceto m ,suponha

e

pode tomar um dos 4 valores exceto

, suponha
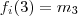
. Estas palavras acima se resume em :

.
Imagine 3 segmentos de retas verticais
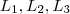
.Marque 4 pontos sobre L_1 , 3 pontos sobre a reta L_2 e 2 sobre a L_3 (em que estes pontos podem ser visto com os valores que m_i podem assumir ,escolhendo um na primeira reta ,na segunda reta terá 3 possibilidades todas distintas da escolha anterior e assim por diante )
Partindo do primeiro ponto de

e escolhendo um caminho dentre os

que há para chegar em um dos pontos de

.Chegando lá , podemos escolher um caminho p/ chegar em um dos pontos de
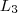
dentre os 3 disponíveis . Para cada procedimento completo nos fornecerá uma aplicação injetiva .Só aqui já conseguimos ,

aplicações injetoras .
Partindo do segundo ponto de

e fazendo o mesmo acima obteremos

aplicações injetoras e assim por diante podemos obter no total

aplicações injetoras .
Acho que agora está certo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Pessoa Estranha » Qua Dez 18, 2013 21:16
por Pessoa Estranha » Qua Dez 18, 2013 21:16
Eu ia questionar exatamente isto. Fiz as contas e, realmente, resultou em 24 e não em 12. Bem, com relação ao caso geral, n e m, vou pensar um pouco mais no que você escreveu e tentar fixar melhor a ideia. Muito obrigada pela ajuda!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Qua Dez 18, 2013 22:47
por e8group » Qua Dez 18, 2013 22:47
Anexei uma imagem neste tópico explicando este processo .
viewtopic.php?p=44888#p44888
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por tenebroso » Qua Dez 18, 2013 22:54
por tenebroso » Qua Dez 18, 2013 22:54
O lucro obtido por um comerciante na venda de determinado produto é dado , em reais, pela função L(x)= -1/10x²+ 15x, sendo x o número de unidades vendidas e o menor que x menor que 150.
Se L(m) é o lucro máximo que comerciante tem condições de obter, pode-se afirmar que log( l(m)/3m) é igual a:
a) 1+2log2
b) 2log2+log5
c) 2-log5 QUEM CONSEGUE RESOLVER? EU NÃO CONSEGUI, ALGUÉM CONSEGUE?
d) 1-2log2
e) 1-2log5
-
tenebroso
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Dez 18, 2013 16:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: estudante
- Andamento: cursando
 por Pessoa Estranha » Qui Dez 19, 2013 08:54
por Pessoa Estranha » Qui Dez 19, 2013 08:54
Olá....
Então, acho que podemos afirmar algo sobre o caso geral. Temos que, se A tem n elementos e B tem r, então, para f : A ----> B, podemos ter o seguinte raciocínio: seja x1 um elemento de A; x1 tem r elementos de B disponíveis para ser sua imagem. Mas, uma vez escolhido um r1 de B, como f deve ser injetora, outro elemento de A, um x2, já não tem mais r opções de imagem e, sim r-1. E isto se repete sucessivamente. Se aplicarmos este raciocínio, teríamos, para um caso geral, r.(r-1).(r-2). ... .(r-(n-1)). Bem, fazendo manipulações algébricas, chega-se à fórmula do Arranjo Ar,n =
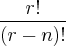
.
Fórmulas, fórmulas, fórmulas e mais fórmulas !!!!
Quando fiz este exercício pela primeira vez, consegui chegar até r.(r-1).(r-2). ... .(r-(n-1)) (e a resposta, é claro, não estava assim), mas nem passou pelo meu raciocínio que era, na verdade, a fórmula do arranjo.
Bem, muito obrigada pela sua ajuda. Consegui fixar melhor o raciocínio. Valeu!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Qui Dez 19, 2013 09:00
por Pessoa Estranha » Qui Dez 19, 2013 09:00
Tenebroso, você tentou resolver o seu exercício ou tem alguma ideia ? Se, até amanhã, ninguém te ajudar, tentarei fazer. Estou olhando os seus exercícios. Aquele de combinatória está bem esquisito, parece que falta informação. Até mais.

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Análise combinatória [exercício]
por Valdemir Oliveira » Sáb Fev 09, 2013 01:23
- 4 Respostas
- 2933 Exibições
- Última mensagem por Valdemir Oliveira

Sáb Fev 09, 2013 21:28
Análise Combinatória
-
- [Analise combinatoria] exercicio
por amanda s » Sex Nov 15, 2013 20:17
- 0 Respostas
- 919 Exibições
- Última mensagem por amanda s

Sex Nov 15, 2013 20:17
Análise Combinatória
-
- [Análise Combinatória] Exercício
por Pessoa Estranha » Qua Dez 11, 2013 17:40
- 1 Respostas
- 1164 Exibições
- Última mensagem por Pessoa Estranha

Qui Dez 12, 2013 20:55
Análise Combinatória
-
- [Análise Combinatória] Exercício
por Pessoa Estranha » Ter Dez 17, 2013 22:27
- 0 Respostas
- 1482 Exibições
- Última mensagem por Pessoa Estranha

Ter Dez 17, 2013 22:27
Análise Combinatória
-
- Análise Combinatória - Dúvida em exercício
por carlosvinnicius » Ter Fev 08, 2011 23:01
- 1 Respostas
- 3008 Exibições
- Última mensagem por MarceloFantini

Ter Fev 08, 2011 23:30
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ) "
) "
 ) "
) "
 e
e  . Considere
. Considere 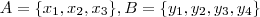 e seja
e seja  o conjunto das aplicações
o conjunto das aplicações injetoras .Notando que
injetoras .Notando que 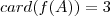 ,poderíamos pensar em quantos subconjuntos (distintos) de
,poderíamos pensar em quantos subconjuntos (distintos) de  possui cardinalidade 3 . Nota :
possui cardinalidade 3 . Nota : 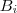 de B com 3 elementos é possível obter o mesmo número de aplicações injetivas tais que
de B com 3 elementos é possível obter o mesmo número de aplicações injetivas tais que 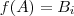 .
.  cuja o conjunto imagem é
cuja o conjunto imagem é  , o que difere cada aplicação é a regra de associação . E a cada par de aplicações cujos conjuntos imagens são respect.
, o que difere cada aplicação é a regra de associação . E a cada par de aplicações cujos conjuntos imagens são respect. 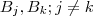 o que difere estas funções são os conjuntos imagens .
o que difere estas funções são os conjuntos imagens . 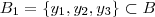 . É possível definir
. É possível definir  aplicações injetivas (distintas) . Ora , se
aplicações injetivas (distintas) . Ora , se 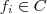 podemos ter
podemos ter 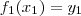 ou
ou  ou ainda
ou ainda  .Assim , basta por
.Assim , basta por  (j=1,2,3) .
(j=1,2,3) . 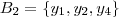
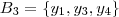
 .
. ).
). injetivas (distintas) , em linguagem de conjunto
injetivas (distintas) , em linguagem de conjunto 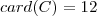 .
. 

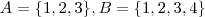 . E defina
. E defina  injetora . Segue-se que
injetora . Segue-se que  pode tomar 4 valores ,
pode tomar 4 valores , 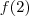 pode tomar 3 valores e
pode tomar 3 valores e 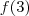 2 valores . Assim o número total de funções injetivas é
2 valores . Assim o número total de funções injetivas é  .
.  injetora .
injetora . 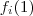 pode tomar 4 valores ,suponha
pode tomar 4 valores ,suponha 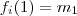 .Então
.Então  pode tomar um dos 4 valores exceto m ,suponha
pode tomar um dos 4 valores exceto m ,suponha  e
e  pode tomar um dos 4 valores exceto
pode tomar um dos 4 valores exceto  , suponha
, suponha 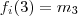 . Estas palavras acima se resume em :
. Estas palavras acima se resume em :  .
.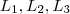 .Marque 4 pontos sobre L_1 , 3 pontos sobre a reta L_2 e 2 sobre a L_3 (em que estes pontos podem ser visto com os valores que m_i podem assumir ,escolhendo um na primeira reta ,na segunda reta terá 3 possibilidades todas distintas da escolha anterior e assim por diante )
.Marque 4 pontos sobre L_1 , 3 pontos sobre a reta L_2 e 2 sobre a L_3 (em que estes pontos podem ser visto com os valores que m_i podem assumir ,escolhendo um na primeira reta ,na segunda reta terá 3 possibilidades todas distintas da escolha anterior e assim por diante ) e escolhendo um caminho dentre os
e escolhendo um caminho dentre os  que há para chegar em um dos pontos de
que há para chegar em um dos pontos de  .Chegando lá , podemos escolher um caminho p/ chegar em um dos pontos de
.Chegando lá , podemos escolher um caminho p/ chegar em um dos pontos de 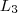 dentre os 3 disponíveis . Para cada procedimento completo nos fornecerá uma aplicação injetiva .Só aqui já conseguimos ,
dentre os 3 disponíveis . Para cada procedimento completo nos fornecerá uma aplicação injetiva .Só aqui já conseguimos ,  aplicações injetoras .
aplicações injetoras .  e fazendo o mesmo acima obteremos
e fazendo o mesmo acima obteremos  aplicações injetoras e assim por diante podemos obter no total
aplicações injetoras e assim por diante podemos obter no total  aplicações injetoras .
aplicações injetoras .




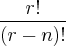 .
.



 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?