Não, não é mentira que

, sabe por quê? Porque

e

. Se ambos fossem menores do que zero, essa propriedade não valeria.
E eu afirmei que
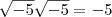
baseado no fato de que

, onde

é a unidade imaginária. Logo,

.
Thadeu, eu reli tudo o que você escreveu nesse tópico, e acho que já sei o que está errado no seu raciocínio.
Você está achando que as propriedades
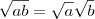
,
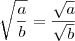
,

, entre outras, são válidas pra
qualquer valor de

,

,

ou

, certo? Pois bem, isso não é verdade. Elas são válidas pra alguns valores, mas inválidas pra outros.
Lembra da famosa
condição de existência? Todas essas propriedades têm uma condição de existência, que quase sempre é ignorada. Até as propriedades mais simples têm condições de existência, mas a gente às vezes nem repara. Por exemplo, as duas propriedades a seguir têm condições de existência:
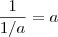
e

Elas parecem sempre corretas, mas veja que a primeira só vale se
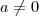
e a segunda só vale se

.
Agora esquecendo esses dois exemplos e voltando ao que interessa, vou enunciar as duas primeiras propriedades junto com suas condições de existência:
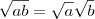 SOMENTE SE
SOMENTE SE  E
E 
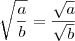 SOMENTE SE
SOMENTE SE  E
E 
Agora, pra finalizar, eu afirmo pra você que
a propriedade  nem sempre é verdadeira
nem sempre é verdadeira, isto é, ela tem, sim, suas condições de existência. Quer ver?
Sejam

e

. Desse modo, a propriedade

equivale a dizer que:

Certo? Ora, essa igualdade só vai ser verdadeira se

e

forem funções inversas uma da outra.
De fato, no caso de

e
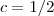
, temos
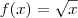
e

, que são funções inversas uma da outra. Certo???
QUASE!!A verdade é que
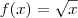
e

são funções inversas
SOMENTE SE 
. Se
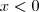
, elas não são inversas.
Portanto, vou enunciar essa propriedade junto com sua condição de existência:
 SOMENTE PARA OS VALORES EM QUE
SOMENTE PARA OS VALORES EM QUE  E
E  SÃO FUNÇÕES INVERSAS
SÃO FUNÇÕES INVERSASO que quer dizer que

e
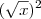
só são iguais se

. Se
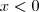
, não são iguais.
Agora você concorda com o que disseram o Lúcio Carvalho e o Elcioschin?

Desculpe pelo texto enorme!
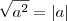
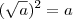 ?
?  (usando a propriedade
(usando a propriedade 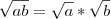 )
)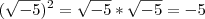
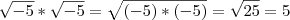 ?
?
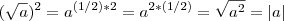 ?
?

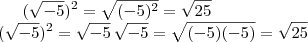
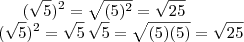
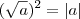 .
.
![\sqrt[]{-4} \sqrt[]{-4}](/latexrender/pictures/0cb2b73b9f0c37e560cd9842492b0a36.png) em IR.
em IR.![{(\sqrt[]{-5})}^{2}\neq\sqrt[]{{(-5)}^{2}} {(\sqrt[]{-5})}^{2}\neq\sqrt[]{{(-5)}^{2}}](/latexrender/pictures/ce279bf1e9bd2b37bc1dfd3865a94a2b.png)


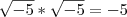

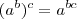
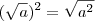 ou que
ou que 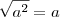 , que não são verdade. ?
, que não são verdade. ?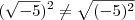 , isso não é verdade. Essa propriedade é verdadeira sim.
, isso não é verdade. Essa propriedade é verdadeira sim. , e que ,muitos autores, consideram
, e que ,muitos autores, consideram 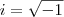 ; teremos:
; teremos:
 é "considerado"
é "considerado"  .
.
 mas acabou de provar que não é, pois concluiu que
mas acabou de provar que não é, pois concluiu que 

 .
. , e "provei" que eles eram diferentes???? (-1 = 1)
, e "provei" que eles eram diferentes???? (-1 = 1)![(\sqrt[m]{x})^n=\sqrt[m]{x^n}\,\,\,,\,\,m \in N\,\,\,e\,\,\,m \geq 2 (\sqrt[m]{x})^n=\sqrt[m]{x^n}\,\,\,,\,\,m \in N\,\,\,e\,\,\,m \geq 2](/latexrender/pictures/bdde20dd502d66764dbeab16f4a5bf77.png) ; hoje usamos o famoso "corte", para resolvermos exercícios mais rapidamente e com isso as propriedades corretas ficam de lado.
; hoje usamos o famoso "corte", para resolvermos exercícios mais rapidamente e com isso as propriedades corretas ficam de lado.![(\sqrt[m]{x})^n=\sqrt[m]{x^n} (\sqrt[m]{x})^n=\sqrt[m]{x^n}](/latexrender/pictures/0e57fd9ab5c3ae12f0ef73019aa7cd42.png) é verdadeira, como tu falou, mostrando o caso do -1=1 se ela não fosse, como então
é verdadeira, como tu falou, mostrando o caso do -1=1 se ela não fosse, como então 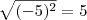 ????
????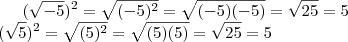
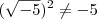
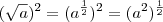 , nesse caso, como pode
, nesse caso, como pode  ser negativo????
ser negativo???? ou, como você escreveu, "jamais"
ou, como você escreveu, "jamais"  .
. ????
????![\sqrt[2]{2}*\sqrt[2]{2} \sqrt[2]{2}*\sqrt[2]{2}](/latexrender/pictures/1df017da7da85e854d79519965788ff2.png)
![({\sqrt[2]{2}})^{2} ({\sqrt[2]{2}})^{2}](/latexrender/pictures/f5d5e0682b1ff12c63ee38ca0c48209b.png)
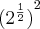
![\sqrt[2]{-2}*\sqrt[2]{-2} \sqrt[2]{-2}*\sqrt[2]{-2}](/latexrender/pictures/431d07f5c9a591eb613f310c582179b5.png)
![({\sqrt[2]{-2}})^{2} ({\sqrt[2]{-2}})^{2}](/latexrender/pictures/ace0b13af3d42c6392f4f3d2dfcc54d6.png)
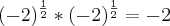

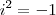 .
.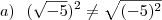

 não é verdadeira...
não é verdadeira...![[(-2)^{\frac{1}{2}}]^2=[(-2)^2]^{\frac{1}{2}} [(-2)^{\frac{1}{2}}]^2=[(-2)^2]^{\frac{1}{2}}](/latexrender/pictures/a09c2dc3eb2fa1006f1ed2f0896a66b7.png)
 é um número imaginário, já
é um número imaginário, já 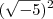 não é.
não é.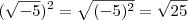 .
. .
.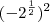 tem base negativa
tem base negativa  com expoente par (2), logo o resultado não pode ser negativo.
com expoente par (2), logo o resultado não pode ser negativo.


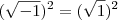
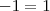
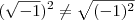 , então está provado que 1 é igual a -1; e isso é correto???
, então está provado que 1 é igual a -1; e isso é correto??? ??? (3ª linha)
??? (3ª linha)
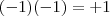
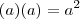

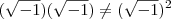 ?????
????? ????
????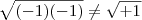 ?????
?????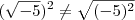 , e isso é
, e isso é 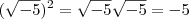 .
.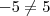 . Esse é o único desenvolvimento correto. Qualquer outro está errado.
. Esse é o único desenvolvimento correto. Qualquer outro está errado.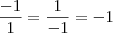 , logo o primeiro e o segundo membros da igualdade são idênticos.
, logo o primeiro e o segundo membros da igualdade são idênticos.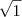 por
por  e
e  por
por  . Fica assim:
. Fica assim: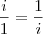
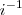 . Fica:
. Fica:
 . Logo, no final das contas, o que a terceira linha afirma é que
. Logo, no final das contas, o que a terceira linha afirma é que  , o que não é verdade.
, o que não é verdade. ???
???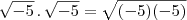 também não é ???
também não é ???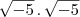 para
para 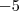 ; baseado em "qual operação" ???
; baseado em "qual operação" ??? , sabe por quê? Porque
, sabe por quê? Porque  e
e  . Se ambos fossem menores do que zero, essa propriedade não valeria.
. Se ambos fossem menores do que zero, essa propriedade não valeria.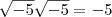 baseado no fato de que
baseado no fato de que  , onde
, onde  .
.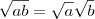 ,
, 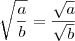 ,
,  ,
,  ,
,  ou
ou  , certo? Pois bem, isso não é verdade. Elas são válidas pra alguns valores, mas inválidas pra outros.
, certo? Pois bem, isso não é verdade. Elas são válidas pra alguns valores, mas inválidas pra outros.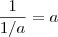

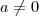 e a segunda só vale se
e a segunda só vale se  .
. E
E 
 e
e  . Desse modo, a propriedade
. Desse modo, a propriedade 
 e
e  forem funções inversas uma da outra.
forem funções inversas uma da outra. e
e 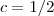 , temos
, temos 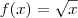 e
e  , que são funções inversas uma da outra. Certo???
, que são funções inversas uma da outra. Certo??? 
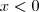 , elas não são inversas.
, elas não são inversas. e
e 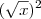 só são iguais se
só são iguais se  ; aqui está sendo colocado
; aqui está sendo colocado 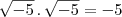 .
. . Isto é:
. Isto é: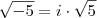
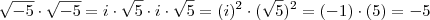
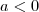 e
e 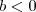 .
. . Nesse caso, você
. Nesse caso, você 
 ? Se não estiver, por que não?
? Se não estiver, por que não?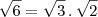 .
.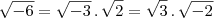 , estaria errado?
, estaria errado? . Isso está
. Isso está  . Pode conferir.
. Pode conferir.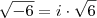

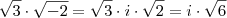
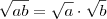 é uma propriedade válida somente quando:
é uma propriedade válida somente quando:
 .
.
 :
: