Estou precisando de ajuda com estas 2 questões..
Esta:

---------------------------------------------------------
E esta :

Podem me ajudar?
Desde ja agradeço (:





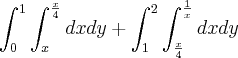
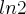

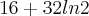


![S=2\pi*\int_{\frac{1}{2}}^{2}4*\sqrt[]{\frac{t^2}{4}+1}dt*\frac{\int_{\frac{1}{2}}^{2}8t*\sqrt[]{t^2+4}dt}{\int_{\frac{1}{2}}^{2}4*\sqrt[]{\frac{t^2}{4}+1}dt} S=2\pi*\int_{\frac{1}{2}}^{2}4*\sqrt[]{\frac{t^2}{4}+1}dt*\frac{\int_{\frac{1}{2}}^{2}8t*\sqrt[]{t^2+4}dt}{\int_{\frac{1}{2}}^{2}4*\sqrt[]{\frac{t^2}{4}+1}dt}](/latexrender/pictures/5eeb00196e3822113ad426fa4c9eaed5.png)
![S=2\pi*\int_{\frac{1}{2}}^{2}t*\sqrt[]{t^2+4}dt S=2\pi*\int_{\frac{1}{2}}^{2}t*\sqrt[]{t^2+4}dt](/latexrender/pictures/f515cb05bd999293070f39b7457f5b68.png)
![S=\frac{2\pi}{3}*(128*\sqrt[]{2}-17*\sqrt[]{17)} S=\frac{2\pi}{3}*(128*\sqrt[]{2}-17*\sqrt[]{17)}](/latexrender/pictures/7459028ebbb7aa6be5d1a9f4c804209c.png)



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.