 por soraaxs » Sáb Nov 30, 2013 22:41
por soraaxs » Sáb Nov 30, 2013 22:41
Ola?
Estou precisando de ajuda com estas 2 questões..
Esta:

---------------------------------------------------------
E esta :

Podem me ajudar?
Desde ja agradeço (:
-
soraaxs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Nov 30, 2013 22:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel Ciencias da Computação
- Andamento: cursando
 por soraaxs » Dom Dez 01, 2013 18:26
por soraaxs » Dom Dez 01, 2013 18:26
Ngm? :(
-
soraaxs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Nov 30, 2013 22:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel Ciencias da Computação
- Andamento: cursando
 por Bravim » Seg Dez 02, 2013 01:02
por Bravim » Seg Dez 02, 2013 01:02
Vou fazer aqui o Desafio 1:
A área do triângulo é dada por:
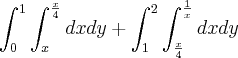
Resolvendo os integrais teremos:
S1=
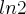
Como o logaritmo de dois é um número transcendente é meio óbvio que é falso, mas é APROXIMADAMENTE igual ao resultado.
Não sei direito como responder a essa questão então vou deixar aí o resultado, mas para mim é falso.
A área da outra figura eu vou fazer da seguinte forma: Calcularei apenas no primeiro quadrante e multiplicarei por 4 para aproveitar a simetria da figura.
S2=

S2=
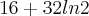
Essa com certeza é falsa. (É possível perceber que é falsa porque só o retângulo [-1,1]x[-4,4] tem uma área maior que 6)
-

Bravim
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Qui Out 03, 2013 03:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por soraaxs » Qua Dez 04, 2013 01:32
por soraaxs » Qua Dez 04, 2013 01:32
Vlw

-
soraaxs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Nov 30, 2013 22:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel Ciencias da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular unidades de área?
por natanlp » Qua Fev 01, 2012 00:45
- 9 Respostas
- 5695 Exibições
- Última mensagem por Arkanus Darondra

Qua Fev 01, 2012 15:34
Geometria Analítica
-
- [INTEGRAIS DUPLAS]Calcular o volume
por Tathiclau » Sex Jan 10, 2014 01:55
- 2 Respostas
- 3135 Exibições
- Última mensagem por Guilherme Pimentel

Seg Jan 13, 2014 06:24
Cálculo: Limites, Derivadas e Integrais
-
- Calcular o volume usando integrais duplas
por Fernandobertolaccini » Dom Jan 11, 2015 17:33
- 1 Respostas
- 3163 Exibições
- Última mensagem por Russman

Dom Jan 11, 2015 19:21
Cálculo: Limites, Derivadas e Integrais
-
- Calcular o volume usando integrais duplas
por Fernandobertolaccini » Dom Jan 11, 2015 17:35
- 3 Respostas
- 4927 Exibições
- Última mensagem por Russman

Seg Jan 12, 2015 16:24
Cálculo: Limites, Derivadas e Integrais
-
- Calcular o volume usando integrais duplas
por Fernandobertolaccini » Dom Jan 11, 2015 17:38
- 0 Respostas
- 2018 Exibições
- Última mensagem por Fernandobertolaccini

Dom Jan 11, 2015 17:38
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







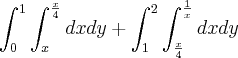
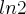

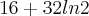


![S=2\pi*\int_{\frac{1}{2}}^{2}4*\sqrt[]{\frac{t^2}{4}+1}dt*\frac{\int_{\frac{1}{2}}^{2}8t*\sqrt[]{t^2+4}dt}{\int_{\frac{1}{2}}^{2}4*\sqrt[]{\frac{t^2}{4}+1}dt} S=2\pi*\int_{\frac{1}{2}}^{2}4*\sqrt[]{\frac{t^2}{4}+1}dt*\frac{\int_{\frac{1}{2}}^{2}8t*\sqrt[]{t^2+4}dt}{\int_{\frac{1}{2}}^{2}4*\sqrt[]{\frac{t^2}{4}+1}dt}](/latexrender/pictures/5eeb00196e3822113ad426fa4c9eaed5.png)
![S=2\pi*\int_{\frac{1}{2}}^{2}t*\sqrt[]{t^2+4}dt S=2\pi*\int_{\frac{1}{2}}^{2}t*\sqrt[]{t^2+4}dt](/latexrender/pictures/f515cb05bd999293070f39b7457f5b68.png)
![S=\frac{2\pi}{3}*(128*\sqrt[]{2}-17*\sqrt[]{17)} S=\frac{2\pi}{3}*(128*\sqrt[]{2}-17*\sqrt[]{17)}](/latexrender/pictures/7459028ebbb7aa6be5d1a9f4c804209c.png)


