 e infelizmente não consegui abrir o caminho para continuar a resolução do problema.
e infelizmente não consegui abrir o caminho para continuar a resolução do problema.Olha só o que tentei:

 e parei aqui.
e parei aqui.Reparem que os termos de uma função racional são bem parecidas e com muita possibilidade de aplicar cancelamento, mas infelizmente eu não estou conseguindo localizar o jeito de continuar na resolução, até tentei pela substituição e nada mudou, continua sobrando uma variável no integrando. Bom, se alguém puder me ajudar, eu agradeço
 Mais tarde vou postar mais dúvidas.
Mais tarde vou postar mais dúvidas.

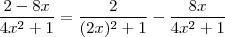 .
.  sabendo-se a integral de
sabendo-se a integral de  (qual é ?) digamos que seja
(qual é ?) digamos que seja 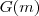 , então pela regra da cadeia
, então pela regra da cadeia ![[G(2x)]' = 2 G'(2x) [G(2x)]' = 2 G'(2x)](/latexrender/pictures/54d141142fd63c152d5a12c4d38a5091.png) .Ora mas isto é exatamente ,
.Ora mas isto é exatamente ,  resolve o problema . Já em relação
resolve o problema . Já em relação 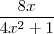 é importante notar que
é importante notar que  é exatamente a derivada de
é exatamente a derivada de  ,então tome
,então tome 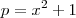 e tente concluir .
e tente concluir .
