 por Victor Mello » Seg Nov 18, 2013 23:04
por Victor Mello » Seg Nov 18, 2013 23:04
Galera, eu estou tentando integrar

e infelizmente não consegui abrir o caminho para continuar a resolução do problema.
Olha só o que tentei:


e parei aqui.
Reparem que os termos de uma função racional são bem parecidas e com muita possibilidade de aplicar cancelamento, mas infelizmente eu não estou conseguindo localizar o jeito de continuar na resolução, até tentei pela substituição e nada mudou, continua sobrando uma variável no integrando. Bom, se alguém puder me ajudar, eu agradeço

Mais tarde vou postar mais dúvidas.
-
Victor Mello
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Nov 03, 2013 17:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da computação.
- Andamento: cursando
 por e8group » Seg Nov 18, 2013 23:27
por e8group » Seg Nov 18, 2013 23:27
Sugestão :
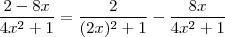
.
As resposta sai de imediato ,em relação

sabendo-se a integral de

(qual é ?) digamos que seja
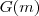
, então pela regra da cadeia
![[G(2x)]' = 2 G'(2x) [G(2x)]' = 2 G'(2x)](/latexrender/pictures/54d141142fd63c152d5a12c4d38a5091.png)
.Ora mas isto é exatamente ,

. É claro que uma substituição simples

resolve o problema . Já em relação
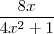
é importante notar que

é exatamente a derivada de

,então tome
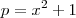
e tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Victor Mello » Ter Nov 19, 2013 00:16
por Victor Mello » Ter Nov 19, 2013 00:16
Consegui agora! Obrigado pela sugestão, e realmente caiu o que você tinha explicado, valeu mesmo!

-
Victor Mello
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Nov 03, 2013 17:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da computação.
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- TECNICAS DE INTEGRAÇÃO
por Marcio Cristo » Qui Dez 22, 2011 18:35
- 5 Respostas
- 3027 Exibições
- Última mensagem por LuizAquino

Sex Dez 23, 2011 18:00
Cálculo: Limites, Derivadas e Integrais
-
- [tecnicas de integraçao por partes (u)(dv)]
por menino de ouro » Ter Out 30, 2012 18:21
- 3 Respostas
- 2077 Exibições
- Última mensagem por MarceloFantini

Ter Out 30, 2012 22:39
Cálculo: Limites, Derivadas e Integrais
-
- [Tecnicas de integraçao por substiuiçao simples]
por menino de ouro » Qua Out 24, 2012 16:12
- 1 Respostas
- 1501 Exibições
- Última mensagem por young_jedi

Qua Out 24, 2012 16:51
Cálculo: Limites, Derivadas e Integrais
-
- Técnicas de integração - multiplicando pelo fator unitário
por Victor Mello » Qui Nov 21, 2013 18:37
- 2 Respostas
- 1708 Exibições
- Última mensagem por Victor Mello

Qui Nov 21, 2013 23:27
Cálculo: Limites, Derivadas e Integrais
-
- [ Inequaçoes Quadráticas-Técnicas]
por R0nny » Qua Mai 01, 2013 17:02
- 0 Respostas
- 1059 Exibições
- Última mensagem por R0nny

Qua Mai 01, 2013 17:02
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e infelizmente não consegui abrir o caminho para continuar a resolução do problema.
e infelizmente não consegui abrir o caminho para continuar a resolução do problema.
 e parei aqui.
e parei aqui. Mais tarde vou postar mais dúvidas.
Mais tarde vou postar mais dúvidas.

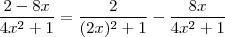 .
.  sabendo-se a integral de
sabendo-se a integral de  (qual é ?) digamos que seja
(qual é ?) digamos que seja 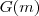 , então pela regra da cadeia
, então pela regra da cadeia ![[G(2x)]' = 2 G'(2x) [G(2x)]' = 2 G'(2x)](/latexrender/pictures/54d141142fd63c152d5a12c4d38a5091.png) .Ora mas isto é exatamente ,
.Ora mas isto é exatamente ,  resolve o problema . Já em relação
resolve o problema . Já em relação 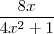 é importante notar que
é importante notar que  é exatamente a derivada de
é exatamente a derivada de  ,então tome
,então tome 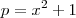 e tente concluir .
e tente concluir .
