3 x + y = 1
2 x - y = 3
RESPOSTA 4/5, -7/5
Preciso saber como chegar nesses resultados, obrigao!
por hatredshadows » Sex Nov 08, 2013 08:17
por e8group » Sex Nov 08, 2013 10:21
.Daí surgi uma pergunta : Será que estas retas são concorrentes ? Ou seja , será que estas retas possuem um ponto em comum ? Ora ,p/ responder esta pergunta verifiquemos se existe pares ordenados (a,b) que satisfaz as duas equações ao mesmo tempo . Vejamos um ponto que satisfaz uma das equações .O ponto 
pertence à reta 
de equação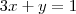 
, pois , substituindo 
por 
e 
por 
em 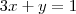,obtemos que 
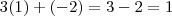. Agora façamos o mesmo na equação 
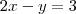,temos , 
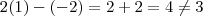.Vemos então que o ponto pertence à reta de equação 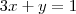, porém o mesmo não pertence à reta 
de equação .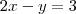
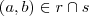,isto 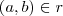é , 
e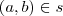 
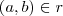. , então 
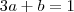,ou de forma equivalente, 
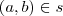. Por outro lado , se então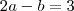 
. Mas vimos acima que ,utilizando este resultado , obtemos 
.Resolvendo esta equação obterá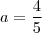 
. Agora substituindo este valor em , segue 
. E de fato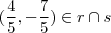 
. Pois, ... deixo p/ vc verificar que este ponto satisfaz ambas equações .
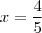e substituindo este resultado em uma das equações obtendo 
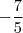. Entretanto ,achei interessante interpretar este sistema geometricamente . Comente as dúvidas .
por hatredshadows » Sex Nov 08, 2013 18:01
por e8group » Sex Nov 08, 2013 20:53
hatredshadows escreveu:Obrigado por responder!
De fato uma interpretação geométrica esclarece muito mais e apresenta uma visão diferenciada da matemática que muitas vezes não aprendemos no ensino regular.
Para encontrar Y, seria:
3 . (4/5) + y = 1
12/5 + y = 1
y = -12/5 + 1
y = -12/5 + 5/5 <-- aqui estava minha dificuldade, esqueci que poderia transformar 1 em 5/5
y= -7/5
Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
zig escreveu:
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.