[Limite] Limite notável

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Limite] Limite notável

Regras do fórum
Responder

[Limite] Limite notável

Mensagempor Nicolas1Lane » Sáb Set 28, 2013 13:13

Questão: \lim_{x\to \ 2} \frac{sen(x)-sen(2)}{x-2}

Eu tenho dúvida quanto a simplificação para o -lim sen(2), neste limite.
Pensei inicialmente que havia obtido o valor correto para as operações, mas percebi que estava enganado quanto a simplificação de -sen(2), então queria simplesmente que me dissessem o caminho para poder realizar esta simplificação.
Quando estava a resolver anteriormente já havia incluído o uso de uma variável y de modo que y=x-2 tal que x=y+2 e logo
\lim_{y\to \ 0} \frac{sen(y+2)-sen(2)}{y}

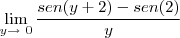
A resposta dada para a questão segundo a lista é cos(2).
Obrigado pelo seu tempo.
Nicolas1Lane
Usuário Ativo
Usuário Ativo
 
Mensagens: 12
Registrado em: Qua Set 11, 2013 23:25
Formação Escolar: ENSINO FUNDAMENTAL I
Área/Curso: Exatas/Ciência da Computação
Andamento: cursando
Voltar ao topo

Re: [Limite] Limite notável

Mensagempor Russman » Sáb Set 28, 2013 16:24

Este limite remete a definição de derivada. Lembre-se que a derivada da função seno é a cosseno.
"Ad astra per aspera."
Russman
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 1183
Registrado em: Sex Abr 20, 2012 22:06
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Física
Andamento: formado
Voltar ao topo

Re: [Limite] Limite notável

Mensagempor Nicolas1Lane » Sáb Set 28, 2013 17:01

Bom, problemático.... eu não vi ainda derivação.
Valeu.
Nicolas1Lane
Usuário Ativo
Usuário Ativo
 
Mensagens: 12
Registrado em: Qua Set 11, 2013 23:25
Formação Escolar: ENSINO FUNDAMENTAL I
Área/Curso: Exatas/Ciência da Computação
Andamento: cursando
Voltar ao topo

Re: [Limite] Limite notável

Mensagempor young_jedi » Sáb Set 28, 2013 18:08

\lim_{x\to2}\frac{\sin(x)-\sin(2)}{x-2}

\lim_{x\to2}\frac{\sin(x-2+2)-\sin(2)}{x-2}

\lim_{x\to2}\frac{\cos(x-2)\sin(2)+\sin(x-2)\cos(2)-\sin(2)}{x-2}

\lim_{x\to2}\frac{(\cos(x-2)-1)\sin(2)}{x-2}+\frac{\sin(x-2)}{x-2}\cos(2)

\lim_{x\to2}\frac{\cos(x-2)+1}{\cos(x-2)+1}\frac{(\cos(x-2)-1)\sin(2)}{x-2}+\frac{\sin(x-2)}{x-2}\cos(2)

\lim_{x\to2}\frac{1}{\cos(x-2)+1}.\frac{(\cos^2(x-2)-1)\sin(2)}{x-2}+\frac{\sin(x-2)}{x-2}\cos(2)

\lim_{x\to2}\frac{1}{\cos(x-2)+1}.\frac{(-\sin^2(x-2))\sin(2)}{x-2}+\frac{\sin(x-2)}{x-2}\cos(2)

\lim_{x\to2}\frac{-\sin(x-2)}{\cos(x-2)+1}.\frac{\sin(x-2)\sin(2)}{x-2}+\frac{\sin(x-2)}{x-2}\cos(2)=\frac{-0.1.\sin(2)}{1+1}+1.\cos(2)=\cos(2)
young_jedi
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 1239
Registrado em: Dom Set 09, 2012 10:48
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Elétrica - UEL
Andamento: formado
Voltar ao topo

Re: [Limite] Limite notável

Mensagempor Nicolas1Lane » Sáb Set 28, 2013 18:22

Muito obrigado.
Nicolas1Lane
Usuário Ativo
Usuário Ativo
 
Mensagens: 12
Registrado em: Qua Set 11, 2013 23:25
Formação Escolar: ENSINO FUNDAMENTAL I
Área/Curso: Exatas/Ciência da Computação
Andamento: cursando
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 


Tópico Popular

Assunto: Exercicios de polinomios
Autor: shaft - Qua Jun 30, 2010 17:30

2x+5=\left(x+m\right)²-\left(x-n \right)²

Então, o exercicio pede para encontrar {m}^{3}-{n}^{3}.

Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !

Assunto: Exercicios de polinomios
Autor: Douglasm - Qua Jun 30, 2010 17:53

Bom, se desenvolvermos isso, encontramos:

2x+5 = 2x(m+n) + m^2-n^2

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):

2(m+n) = 2 \;\therefore\; m+n = 1

m^2-n^2 = 5 \;\therefore\; (m+n)(m-n) = 5 \;\therefore\; (m-n) = 5

Somando a primeira e a segunda equação:

2m = 6 \;\therefore\; m = 3 \;\mbox{consequentemente:}\; n=-2

Finalmente:

m^3 - n^3 = 27 + 8 = 35

Até a próxima.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

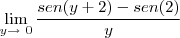
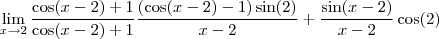
Índice do fórum