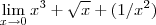
e também este:
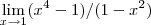
Obrigado.

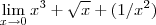
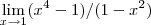

 , portanto você irá obter como resposta uma função tendendo a
, portanto você irá obter como resposta uma função tendendo a  .
. ou -
ou - , através dos limites laterais, mas como
, através dos limites laterais, mas como  , logo por qualquer lado será positivo e a resposta será +
, logo por qualquer lado será positivo e a resposta será + .
. , portanto você deve utilizar alguma técnica (fatoração por exemplo) para eliminar a indeterminação:
, portanto você deve utilizar alguma técnica (fatoração por exemplo) para eliminar a indeterminação: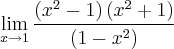
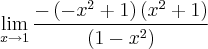
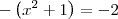

Sobreira escreveu:Note que no primeiro exemplo você terá uma indeterminação do tipo, portanto você irá obter como resposta uma função tendendo a
.
Você pode verificar se a função tende a +ou -
, através dos limites laterais, mas como
, logo por qualquer lado será positivo e a resposta será +
.
No segundo exemplo há uma indeterminação do tipo, portanto você deve utilizar alguma técnica (fatoração por exemplo) para eliminar a indeterminação:
 ?
?

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes

 .
.



