PRECISO DE AJUDA URGENTE, POR FAVOR!
Tenho a seguinte questão para fazer usando o teorema de Rolle: sen 2 ? x ; [-1,1]
Meu professor me ensinou da seguinte maneira usando condições:
i: f é contínua em [-1,1]
ii: f'(x)= 2 ? cos (2 ? x)
(Até aqui nao tenho dúvidas porem na etapa seguinte dá dois números diferentes pelas minhas contas, um negativo e um positivo, e eu só aprendi a lidar com números iguais)
iii: f(-1)= sen 2 ? (-1)= -0,109387346
f(1)= sen 2 ? 1= 0,109387346 (Resultados diferentes)
Se dessem iguais eu faria da seguinte maneira:
Então ? C ? ]-1,1[ / f'(C)=0
f'(C)= sen 2 ? C
sen 2 ? C=0 (a partir dessa parte também nao consigo resolver, não consigo isolar o C e achar seu(s) resultado(s))
Agradeço a atenção


 tais que
tais que 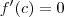 . Tente restringir o intervalo para
. Tente restringir o intervalo para ![[-1,0] \cup [0,1] [-1,0] \cup [0,1]](/latexrender/pictures/f15f556f11fbe947435fffab3ae76ccb.png) .
.
![[-1,-\frac{1}{2}]\cup [-\frac{1}{2},0]\cup [0,\frac{1}{2}]\cup [\frac{1}{2},1] [-1,-\frac{1}{2}]\cup [-\frac{1}{2},0]\cup [0,\frac{1}{2}]\cup [\frac{1}{2},1]](/latexrender/pictures/906784053d7b4a2cce449bc370453fc7.png)




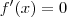 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)