 por Rebecafer » Qua Ago 14, 2013 15:38
por Rebecafer » Qua Ago 14, 2013 15:38
PRECISO DE AJUDA URGENTE, POR FAVOR!
Tenho a seguinte questão para fazer usando o teorema de Rolle: sen 2 ? x ; [-1,1]
Meu professor me ensinou da seguinte maneira usando condições:
i: f é contínua em [-1,1]
ii: f'(x)= 2 ? cos (2 ? x)
(Até aqui nao tenho dúvidas porem na etapa seguinte dá dois números diferentes pelas minhas contas, um negativo e um positivo, e eu só aprendi a lidar com números iguais)
iii: f(-1)= sen 2 ? (-1)= -0,109387346
f(1)= sen 2 ? 1= 0,109387346 (Resultados diferentes)
Se dessem iguais eu faria da seguinte maneira:
Então ? C ? ]-1,1[ / f'(C)=0
f'(C)= sen 2 ? C
sen 2 ? C=0 (a partir dessa parte também nao consigo resolver, não consigo isolar o C e achar seu(s) resultado(s))
Agradeço a atenção
-
Rebecafer
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Ago 13, 2013 17:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Faculdade de Engenharia Civil
- Andamento: cursando
 por Russman » Qua Ago 14, 2013 21:31
por Russman » Qua Ago 14, 2013 21:31
É que nesse intervalo existem dois pontos

tais que
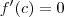
. Tente restringir o intervalo para
![[-1,0] \cup [0,1] [-1,0] \cup [0,1]](/latexrender/pictures/f15f556f11fbe947435fffab3ae76ccb.png)
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Rebecafer » Qui Ago 15, 2013 11:24
por Rebecafer » Qui Ago 15, 2013 11:24
E como faço essa conta? Meu prefessor nao me ensinou a usar esse método ainda, esse exercício que ele passou é um desafio.
-
Rebecafer
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Ago 13, 2013 17:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Faculdade de Engenharia Civil
- Andamento: cursando
 por Russman » Qui Ago 15, 2013 13:12
por Russman » Qui Ago 15, 2013 13:12
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Rebecafer » Qui Ago 15, 2013 18:10
por Rebecafer » Qui Ago 15, 2013 18:10
Como utilizo a União?
-
Rebecafer
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Ago 13, 2013 17:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Faculdade de Engenharia Civil
- Andamento: cursando
 por Russman » Qui Ago 15, 2013 22:11
por Russman » Qui Ago 15, 2013 22:11
Se em cada intervalo que eu citei existe

tal que
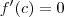
, então o teorema se aplica também ao intervalo unido. Certo ? No intervalo todo existem 4 pontos que satisfazem
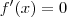
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Rebecafer » Qui Ago 15, 2013 23:57
por Rebecafer » Qui Ago 15, 2013 23:57
Agora entendi, esta certo, muito obrigada.
-
Rebecafer
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Ago 13, 2013 17:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Faculdade de Engenharia Civil
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema de Rolle
por Mel92 » Sex Nov 23, 2012 23:57
- 5 Respostas
- 3399 Exibições
- Última mensagem por Mel92

Sáb Nov 24, 2012 18:44
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida teorema de Rolle
por pedro30 » Sáb Abr 20, 2013 12:55
- 1 Respostas
- 1281 Exibições
- Última mensagem por e8group

Sáb Abr 20, 2013 14:01
Cálculo: Limites, Derivadas e Integrais
-
- Derivada teorema de Rolle
 por juflamanto » Sáb Out 10, 2015 21:24
por juflamanto » Sáb Out 10, 2015 21:24
- 1 Respostas
- 1201 Exibições
- Última mensagem por adauto martins

Sex Out 30, 2015 12:24
Cálculo: Limites, Derivadas e Integrais
-
- [Teorema de Fermat] Problema
por dravz » Seg Fev 25, 2013 01:55
- 1 Respostas
- 1005 Exibições
- Última mensagem por Russman

Seg Fev 25, 2013 03:15
Cálculo: Limites, Derivadas e Integrais
-
- Teorema de Pitágoras - Problema
 por ALPC » Qua Mai 22, 2013 17:50
por ALPC » Qua Mai 22, 2013 17:50
- 4 Respostas
- 7143 Exibições
- Última mensagem por ALPC

Dom Mai 26, 2013 00:20
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 tais que
tais que 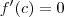 . Tente restringir o intervalo para
. Tente restringir o intervalo para ![[-1,0] \cup [0,1] [-1,0] \cup [0,1]](/latexrender/pictures/f15f556f11fbe947435fffab3ae76ccb.png) .
.
![[-1,-\frac{1}{2}]\cup [-\frac{1}{2},0]\cup [0,\frac{1}{2}]\cup [\frac{1}{2},1] [-1,-\frac{1}{2}]\cup [-\frac{1}{2},0]\cup [0,\frac{1}{2}]\cup [\frac{1}{2},1]](/latexrender/pictures/906784053d7b4a2cce449bc370453fc7.png)




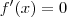 .
.