por favor quem souber resolva ou pelo menos alguma sugestão
desde ja fico grato...
para todo n positivo, seja
 ovalor mínimo da soma :
ovalor mínimo da soma : 
![\sqrt[]{(k-1)²+ak²} \sqrt[]{(k-1)²+ak²}](/latexrender/pictures/801f7567ac1c51d466bf588bff446099.png) , onde
, onde  ,
,  , ...,
, ...,  são numeros reais positivos cuja soma é igual a 17. sabendo que existe um único número inteiro positivo n para o qual
são numeros reais positivos cuja soma é igual a 17. sabendo que existe um único número inteiro positivo n para o qual  é também um número inteiro , o valor de n é igual a :
é também um número inteiro , o valor de n é igual a :a)10
b)12
c)15
d)16
e)17
não sei explicar ,mas o  dentro da raiz (a maiúsculo não existe na expressao )!!!!!!!!!!!!!! a expressão (2k-1)²+ak² existe mas o  não existe


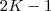 e
e 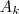
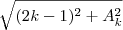
 portanto um dos catetos desse triangulo é 17 e o outro é dado pela soma
portanto um dos catetos desse triangulo é 17 e o outro é dado pela soma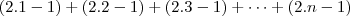
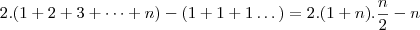
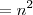
 então a hipotenusa que é igual ao somatório que queremos encontrar é dada por
então a hipotenusa que é igual ao somatório que queremos encontrar é dada por
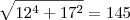

 .
. ) de catetos
) de catetos 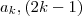 e hipotenusa
e hipotenusa 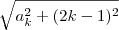 (que vamos designar por
(que vamos designar por 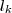 ) semelhantes . Evidenciando a constante de proporcionalidade dos lados dos triângulos
) semelhantes . Evidenciando a constante de proporcionalidade dos lados dos triângulos  concluímos que o triângulo retângulo de catetos
concluímos que o triângulo retângulo de catetos 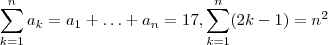 e hipotenusa
e hipotenusa 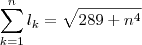 é semelhante a todos triângulos retângulos
é semelhante a todos triângulos retângulos  .
.  natural de modo que ,
natural de modo que , 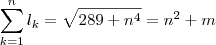 . Elevando ao quadrado e simplificando ,
. Elevando ao quadrado e simplificando , 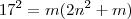 . Aqui cabe analisar se
. Aqui cabe analisar se 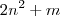 divide
divide 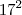 .É fácil verificar que
.É fácil verificar que 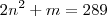 (pois caso fosse
(pois caso fosse 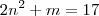 chegaríamos em um absurdo
chegaríamos em um absurdo uma vez que
uma vez que 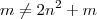 ) . Daí obtemos
) . Daí obtemos 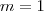 e portanto
e portanto  .
.
 .
.



