 por Geriane07 » Qui Ago 08, 2013 12:23
por Geriane07 » Qui Ago 08, 2013 12:23
Estou em dúvida sobre a questão de anagrama. Fiz várias tentativas, mas não chegou ao resultado dado.
- Considerando a palavra MARKETING, calcule o número total de anagramas que possuem as consoantes todas juntas e em ordem alfabética.
a) 9!
b) 6
c) 120
d) 24
e) 7!
As minhas respostas deram 6 e 84, e a resposta correta é a alternativa d) 24.
Para quem me ajudar, desde já obrigada pela atenção!!!
-
Geriane07
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Ago 08, 2013 12:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: cursando
 por DanielFerreira » Sex Ago 09, 2013 07:05
por DanielFerreira » Sex Ago 09, 2013 07:05
Geriane,
bom dia!
Consideremos as consoantes todas juntas e em ordem alfabética como se fossem apenas uma letra, veja:
GKMNRT.
Portanto, devemos permutar um total de 4 letras, são elas: GKMNRT, A, E, I.
Logo,
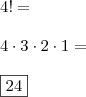
Espero ter ajudado!
Qualquer dúvida comente.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Geriane07 » Ter Ago 13, 2013 13:02
por Geriane07 » Ter Ago 13, 2013 13:02
Obrigada por ter me ajudado, vlw!!!
-
Geriane07
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Ago 08, 2013 12:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: cursando
 por DanielFerreira » Sáb Nov 02, 2013 09:06
por DanielFerreira » Sáb Nov 02, 2013 09:06
Não há de quê!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Anagrama
por Igor » Sex Set 30, 2011 18:02
- 0 Respostas
- 1912 Exibições
- Última mensagem por Igor

Sex Set 30, 2011 18:02
Estatística
-
- Dúvida anagrama
por renataf » Ter Dez 07, 2010 08:47
- 2 Respostas
- 2273 Exibições
- Última mensagem por renataf

Dom Jan 02, 2011 13:45
Estatística
-
- Permutação-Anagrama
por Alessandra Cezario » Ter Jan 31, 2012 13:32
- 1 Respostas
- 1723 Exibições
- Última mensagem por Arkanus Darondra

Ter Jan 31, 2012 14:20
Estatística
-
- [Anagrama Simples]
por gustavowelp » Sáb Ago 11, 2012 01:39
- 2 Respostas
- 1733 Exibições
- Última mensagem por gustavowelp

Qua Ago 15, 2012 23:48
Análise Combinatória
-
- [Anagrama Simples]
por gustavowelp » Sex Nov 02, 2012 12:31
- 1 Respostas
- 1645 Exibições
- Última mensagem por young_jedi

Sex Nov 02, 2012 12:46
Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


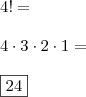



 , avisa que eu resolvo.
, avisa que eu resolvo.

