 por Jhonata » Qui Jul 18, 2013 19:12
por Jhonata » Qui Jul 18, 2013 19:12

Não estou conseguindo resolver este exercício:
Considere os vetores: {(1,1,2),(2,-1,4),(2,4,4)}. Encontre um vetor norma 1 ortogonal aos 3 vetores dados e então, determine módulo da soma de suas entradas.
Gabarito:

Por favor, se alguém puder me ajudar, mesmo que uma sugestão, ficarei grato.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por MateusL » Qui Jul 18, 2013 19:20
por MateusL » Qui Jul 18, 2013 19:20
Dois vetores são ortogonais quando o produto escalar deles é igual a zero.
Chame o vetor que você quer descobrir de (x,y,z), depois escreva o produto escalar deste vetor por cada um dos outros vetores e iguale cada um desses produtos a zero.
Tu vais ter um sistema de três variáveis e três equações.
Resolva o sistema e depois é só aplicar a restrição da norma ser igual a 1.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhonata » Qui Jul 18, 2013 19:39
por Jhonata » Qui Jul 18, 2013 19:39
MateusL escreveu:Dois vetores são ortogonais quando o produto escalar deles é igual a zero.
Chame o vetor que você quer descobrir de (x,y,z), depois escreva o produto escalar deste vetor por cada um dos outros vetores e iguale cada um desses produtos a zero.
Tu vais ter um sistema de três variáveis e três equações.
Resolva o sistema e depois é só aplicar a restrição da norma ser igual a 1.
Abraço!
Obrigado, vou tentar aqui.
Um grande abraço!
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por Jhonata » Qui Jul 18, 2013 20:14
por Jhonata » Qui Jul 18, 2013 20:14
Certo, encontrei o sistema:



Tentando resolver isso, encontro um sistema com infinitas soluções, e então?
Obrigado.
Att.
Editado pela última vez por
Jhonata em Qui Jul 18, 2013 20:21, em um total de 1 vez.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por MateusL » Qui Jul 18, 2013 20:20
por MateusL » Qui Jul 18, 2013 20:20
Isso aí!
Agora escolha uma variável qualquer e escreva as outras duas em função dela.
Por exemplo, vamos supor que tu escrevas x e y em função de z.
Depois faça

(porque no enunciado diz que a norma é igual a 1), substituindo x e y pela escrita deles em função de

.
Resolvendo isso, irás encontrar um valor para

(talvez dois valores) e, consequentemente, encontrarás valores para

e

.
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhonata » Qui Jul 18, 2013 20:30
por Jhonata » Qui Jul 18, 2013 20:30
Ainda acho que estou fazendo algo errado.
Escalonei a matriz associada ao sistema anterior e obtive que:
y = 0, x=-2z, tomando z = t, então x = -2t.
Então, uma base para esse conjunto ortonormal seria (-2,0,1) (tomando t =1).
Como a norma é 1, as coordenadas desse vetor não batem.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por MateusL » Qui Jul 18, 2013 20:37
por MateusL » Qui Jul 18, 2013 20:37
Quase isso.
Encontrastes

e

pode tomar qualquer valor.
Então as soluções do sistema (os vetores) são da forma

.
Queres encontrar o módulo da soma das entradas, que será

Sabendo que a norma do vetor deve ser igual a

, podes escrever que:

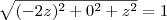

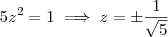
Como sabes que o módulo da soma das entradas vai ser igual a

, esta soma será igual a

Editado pela última vez por
MateusL em Qui Jul 18, 2013 20:47, em um total de 2 vezes.
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhonata » Qui Jul 18, 2013 20:41
por Jhonata » Qui Jul 18, 2013 20:41
Ahhh! Nem imaginava que eu deveria, no fim, encontrar a coordenada Z.
Aparentemente estranho, mas faz muito sentido.
Muito obrigado cara! Pela dedicação, em primeiro lugar, pela atenção e pela maravilhosa ajuda!
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por MateusL » Qui Jul 18, 2013 20:48
por MateusL » Qui Jul 18, 2013 20:48
Na verdade, ao resolveres o sistema, encontras a equação paramétrica de uma reta, a qual é ortogonal aos três vetores dados. Depois disso, tens que encontrar para quais valores do parâmetro tu terás um vetor de norma unitária. Encontrarás dois valores para o parâmetro, porque existem, sobre essa reta, dois vetores que satisfazem as condições.
De nada cara!
Abração!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 Não estou conseguindo resolver este exercício:
Não estou conseguindo resolver este exercício:





 (porque no enunciado diz que a norma é igual a 1), substituindo x e y pela escrita deles em função de
(porque no enunciado diz que a norma é igual a 1), substituindo x e y pela escrita deles em função de  .
. e
e  .
. e
e  .
.
 , podes escrever que:
, podes escrever que: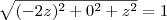

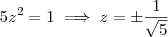
 , esta soma será igual a
, esta soma será igual a 
