


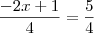
jamiel escreveu:Sabe-se que a parábola que representa a função y = -x²+bx+c passa pelo ponto (3; -5) e que seu vértice é (m; 5/4). Calcule b, c e m.
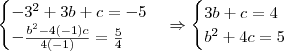
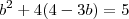 para encontrar b' e b''. Com esses valores você pode calcular c', c'', m' e m''.
para encontrar b' e b''. Com esses valores você pode calcular c', c'', m' e m''.


jamiel escreveu:rsrsrsrs
Caramba! Isso é complicado, viu. Quer dizer q pelo simples fato de uma das equações está com "b²" era pra eu ter deduzido a sua resolução integrando-as para formar uma nova equação, só q em "b"?




jamiel escreveu:Obrigado mais uma vez. Agora, eu tenho ouvido, não é de hoje, as pessoas falarem em "método". Existe algum material, livro com métodos matemáticos, vc poderia me dar uma dica acerca disso?
Calcule os valores de b e c, sabendo que a parábola que representa a função f(x) = x² + bx + c tem vértice (3/2;-1/4).

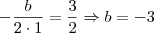
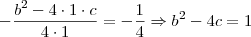


 não é negativo e como você conceguil cancelar os denominadores sendo que um é positivo e outro negativo!!?
não é negativo e como você conceguil cancelar os denominadores sendo que um é positivo e outro negativo!!?

Maria Tamires escreveu:Luis eu não consegui entender a sua resolução
por favor, você pode me explica* porque no seu último sistema onão é negativo e como você conceguil** cancelar os denominadores sendo que um é positivo e outro negativo!!?
Obrigada
Lembretes
* explicar
** conseguiu
 ?
?
![(-1)\left[\frac{b^2-4(-1)c}{4(-1)}\right] = \frac{5}{4} (-1)\left[\frac{b^2-4(-1)c}{4(-1)}\right] = \frac{5}{4}](/latexrender/pictures/82817b2b3fcd68f668b8dba04046f6d5.png)
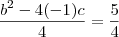
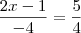

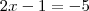





Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.