 por jamiel » Sáb Abr 23, 2011 13:28
por jamiel » Sáb Abr 23, 2011 13:28
Sabe-se que a parábola que representa a função y = -x²+bx+c passa pelo ponto (3;5) e que seu vértice é (m;5/4). Calcule b,c e m.
-b/2•(-1) = m (1)
-?/4•(-1) = 5/4 ---- 5/4•-4 = -20/4 = -5² = ?25 = 5 --->
-[b² -4•(-1)•c] / 4•(-1) = 5/4
b² -4c("?25 =5") = 5 (2)
-(3)² + 3b + c = -5
-9 + 3b + c = -5
3b + c = 4 (3)
Sistema ---->
b² + 4c = 5
3b + c = 4
Aqui é q eu não consegui ir adiante. Se eu considerar o "c=4", obtenho o valor de b²=-11 ---- -11/-2 = "m = 11/2". Porém, não senti precisão, mais, teria q obter mais um "c=-29", o q seria meio contraditório. A coordenadas são (11;-29) e (1;1), no gabarito!
Alguém pode me ajudar nessa? Agrandeço desde já!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por LuizAquino » Sáb Abr 23, 2011 13:54
por LuizAquino » Sáb Abr 23, 2011 13:54
jamiel escreveu:Sabe-se que a parábola que representa a função y = -x²+bx+c passa pelo ponto (3; -5) e que seu vértice é (m; 5/4). Calcule b, c e m.
Observação: No texto original do exercício a parábola passa pelo ponto (3; -5) ou (3; 5)? Se ela passa pelo ponto (3; -5) então é necessário resolver o sistema:
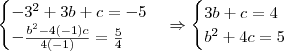
Agora, basta resolver a equação
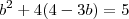
para encontrar b' e b''. Com esses valores você pode calcular c', c'', m' e m''.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jamiel » Sáb Abr 23, 2011 14:16
por jamiel » Sáb Abr 23, 2011 14:16
Desculpa! (3;-5). Mas eu não estou encontrando lógica nesse sistema, fique intrigado com isso.
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Sáb Abr 23, 2011 14:22
por jamiel » Sáb Abr 23, 2011 14:22
rsrsrsrs
Caramba! Isso é complicado, viu. Quer dizer q pelo simples fato de uma das equações está com "b²" era pra eu ter deduzido a sua resolução integrando-as para formar uma nova equação, só q em "b"?
Atualmente, estou cursando Lic. Química, mas estou entusiasmado com a matemática. Pretendo mudar para matemática ou física.
Thank you!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por LuizAquino » Sáb Abr 23, 2011 14:29
por LuizAquino » Sáb Abr 23, 2011 14:29
jamiel escreveu:rsrsrsrs
Caramba! Isso é complicado, viu. Quer dizer q pelo simples fato de uma das equações está com "b²" era pra eu ter deduzido a sua resolução integrando-as para formar uma nova equação, só q em "b"?
Eu apenas usei o método da substituição, no qual isolamos uma incógnita em uma das equações e substituímos na outra equação (neste caso, eu isolei c na primeira equação). Desse modo, geramos uma nova equação com apenas uma incógnita (neste caso, com apenas b). Após ter determinado o valor dessa incógnita (no caso, b), nós usamos qualquer uma das equações originais para determinar o valor da outra incógnita (ou seja, c).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jamiel » Sáb Abr 23, 2011 14:36
por jamiel » Sáb Abr 23, 2011 14:36
Obrigado mais uma vez. Agora, eu tenho ouvido, não é de hoje, as pessoas falarem em "método". Existe algum material, livro com métodos matemáticos, vc poderia me dar uma dica acerca disso?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Sáb Abr 23, 2011 15:31
por jamiel » Sáb Abr 23, 2011 15:31
Tentei resolver com o mesmo método, mas não consegui.
Calcule os valores de b e c, sabendo que a parábola que representa a função f(x) = x² + bx + c tem vértice (3/2;-1/4).
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Sáb Abr 23, 2011 16:42
por jamiel » Sáb Abr 23, 2011 16:42
Eu acho q consegui!
x² + bc + c ---- os vértices(3/2;-1/4)
-b/2•1 = 3/2, como o resultado é positivo, tem-se:3/2•2 = 3"-b"-(-3)/2 = 3/2. o valor "b"
(3/2)² + 3/2b + c = -1/4
9/4 - 3/2•(-3) + c = -1/4
9/4 -9/2 + c = -1/4
c = -1/4 -9/4 + 9/2
c = -5/2 + 9/2
c = 2
Os valores de b e c, respectivamente, são -3 e 2. Não consegui resolver com o mesmo método da anterior!
vlw...
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por LuizAquino » Sáb Abr 23, 2011 21:05
por LuizAquino » Sáb Abr 23, 2011 21:05
jamiel escreveu:Obrigado mais uma vez. Agora, eu tenho ouvido, não é de hoje, as pessoas falarem em "método". Existe algum material, livro com métodos matemáticos, vc poderia me dar uma dica acerca disso?
São três métodos básicos vistos na (antiga) 7ª ou 8ª séries:
- método da substituição;
- método da comparação;
- método da soma.
Com certeza você deve achar muito material sobre isso apenas usando uma ferramenta de pesquisa, como o Google por exemplo.
Calcule os valores de b e c, sabendo que a parábola que representa a função f(x) = x² + bx + c tem vértice (3/2;-1/4).
Note que a partir dos dados do problema você pode obter três equações:
(i)

(ii)
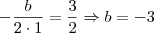
(iii)
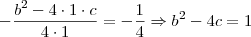
Se você decidir usar (i) e (iii), então você teria um sistema que obviamente poderia ser resolvido usando o método da substituição. Entretanto, é mais inteligente nesse caso usar (ii) e (i) ou (ii) e (iii), já que por (ii) já temos o valor de b.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por jamiel » Sáb Abr 23, 2011 22:12
por jamiel » Sáb Abr 23, 2011 22:12
Bastante esclarecedora sua explicação. Obrigado, mesmo, mais uma vez!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por Maria Tamires » Qui Jul 11, 2013 13:22
por Maria Tamires » Qui Jul 11, 2013 13:22
Luis eu não consegui entender a sua resolução
por favor, você pode me explica porque no seu último sistema o

não é negativo e como você conceguil cancelar os denominadores sendo que um é positivo e outro negativo!!?
Obrigada

-
Maria Tamires
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 11, 2013 09:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3°
- Andamento: cursando
 por LuizAquino » Qui Jul 11, 2013 14:15
por LuizAquino » Qui Jul 11, 2013 14:15
Maria Tamires escreveu:Luis eu não consegui entender a sua resolução
por favor, você pode me
explica* porque no seu último sistema o

não é negativo e como você
conceguil** cancelar os denominadores sendo que um é positivo e outro negativo!!?
Obrigada
 Lembretes
Lembretes* explicar
** conseguiu
Você está se referindo a última equação do primeiro exercício? No caso, a equação

?
Se esta for sua dúvida, note que:

![(-1)\left[\frac{b^2-4(-1)c}{4(-1)}\right] = \frac{5}{4} (-1)\left[\frac{b^2-4(-1)c}{4(-1)}\right] = \frac{5}{4}](/latexrender/pictures/82817b2b3fcd68f668b8dba04046f6d5.png)
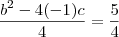
Agora tente continuar a partir daí.
ObservaçãoNão há problema algum se "um denominador é positivo e o outro é negativo".
Por exemplo, suponha que você precisa resolver a seguinte equação:
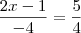
Note que se você multiplicar ambos os membros por -4, você ficará com:

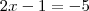
A partir daí, fica fácil obter x = -2.
Uma outra opção seria começar multiplicando o numerador e o denominador da primeira fração por (-1), ficando assim com:

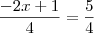

Obviamente obtemos outra vez x = -2.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Maria Tamires » Qui Jul 11, 2013 14:25
por Maria Tamires » Qui Jul 11, 2013 14:25
Nossa como sou tapada kkkkk
Obrigada, ajudou muito!

-
Maria Tamires
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 11, 2013 09:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3°
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolução de sistema
por rei01 » Ter Abr 19, 2011 16:58
- 1 Respostas
- 1640 Exibições
- Última mensagem por NMiguel

Ter Abr 19, 2011 17:46
Sistemas de Equações
-
- Resolução de Um sistema Linear
por fttofolo » Qua Set 21, 2011 19:30
- 2 Respostas
- 4561 Exibições
- Última mensagem por fttofolo

Qua Set 21, 2011 21:47
Sistemas de Equações
-
- [Sistema Não-Linear de Equação] Resolução
por mdiego » Qui Jul 05, 2012 00:14
- 0 Respostas
- 4243 Exibições
- Última mensagem por mdiego

Qui Jul 05, 2012 00:14
Sistemas de Equações
-
- [Sistema Linear] Dúvida na Resolução
por oliveiracosmo » Sáb Set 01, 2012 19:03
- 3 Respostas
- 5447 Exibições
- Última mensagem por DanielFerreira

Seg Set 03, 2012 19:31
Sistemas de Equações
-
- [RESOLUÇÃO DO SISTEMA COMO ELE CHEGOU A ESSE VALOR]
 por osmarioe » Sex Mai 01, 2015 19:20
por osmarioe » Sex Mai 01, 2015 19:20
- 2 Respostas
- 2807 Exibições
- Última mensagem por osmarioe

Sáb Mai 02, 2015 14:21
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



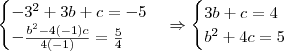
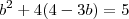 para encontrar b' e b''. Com esses valores você pode calcular c', c'', m' e m''.
para encontrar b' e b''. Com esses valores você pode calcular c', c'', m' e m''.







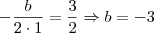
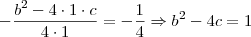


 não é negativo e como você conceguil cancelar os denominadores sendo que um é positivo e outro negativo!!?
não é negativo e como você conceguil cancelar os denominadores sendo que um é positivo e outro negativo!!?

não é negativo e como você conceguil** cancelar os denominadores sendo que um é positivo e outro negativo!!?
 ?
?
![(-1)\left[\frac{b^2-4(-1)c}{4(-1)}\right] = \frac{5}{4} (-1)\left[\frac{b^2-4(-1)c}{4(-1)}\right] = \frac{5}{4}](/latexrender/pictures/82817b2b3fcd68f668b8dba04046f6d5.png)
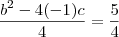
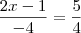

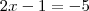






 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?