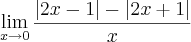
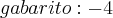
eu não entendi a questão,já resolvi vários limites, mas com somente um módulo,alguém pode me dar uma dica?

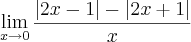
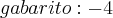

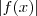 ,onde
,onde  é uma função elementar .Por definição de módulo , segue-se que
é uma função elementar .Por definição de módulo , segue-se que 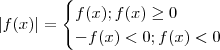 .
.  e
e  para
para  em uma vizinhança do número zero .Se nesta vizinhança ,tem-se
em uma vizinhança do número zero .Se nesta vizinhança ,tem-se 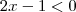 ,segue da definição que
,segue da definição que 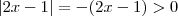 .De forma análoga podemos estudar o outro módulo .Tente concluir .
.De forma análoga podemos estudar o outro módulo .Tente concluir .
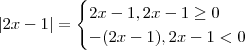
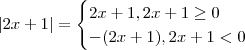

 é negativo ou positivo para
é negativo ou positivo para  em
em ![(-r,r) [tex] com [tex] r > 0 (-r,r) [tex] com [tex] r > 0](/latexrender/pictures/c96defbfb5ad523420d6a6ede8f259ae.png) suficiente pequeno . Da mesma forma façamos a mesma análise para
suficiente pequeno . Da mesma forma façamos a mesma análise para  .
. 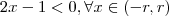 e
e 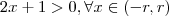 .
. 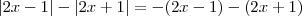 .
. 

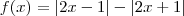 .
.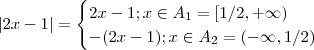
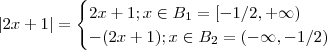
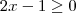 e
e 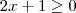
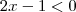 e
e 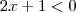
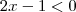 e
e 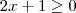
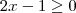 e
e 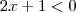
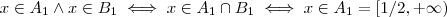 ,no segundo ,
,no segundo , 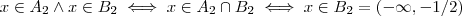 ; terceiro ,segue
; terceiro ,segue 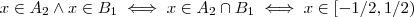 e no último caso , a interseção é vazia .
e no último caso , a interseção é vazia .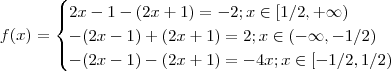 .
.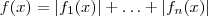 .Por definição de módulo , por exemplo se
.Por definição de módulo , por exemplo se 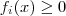 para todo
para todo  .Poderíamos definir ,
.Poderíamos definir , 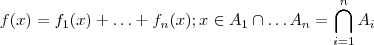




Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)