 por R0nny » Sex Mai 03, 2013 15:12
por R0nny » Sex Mai 03, 2013 15:12
Problema 1:Durante uma experiencia foi registada a variaçao da temperatura de um líquido, em graus celsius, que evoluiu, nas primeiras 8 horas, segundo a funçao:h(t)= x²/4+3x+7 Determine em que momentos da experincia o líquido obteve uma temperatura superior a 10C. Fonte: Pergunta questionada pelo Professor na sala de aula. Se diz em que momentos, está a referir o tempo ou seja o instante, logo se diz que a temperatura superior a 10 graus celcius entao, eu peguei a equaçao e fiz: x²/4+3x+7>10, depois haverá o calculo do delta, só que nao dará uma raiz perfeita. Onde estou falhando??

-
R0nny
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Abr 28, 2013 10:53
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Estudante
- Andamento: cursando
 por young_jedi » Sáb Mai 04, 2013 00:35
por young_jedi » Sáb Mai 04, 2013 00:35
nos meus cálculos delta resultou em 12
realmente não tem raiz exata, você pode deixar a resposta em função da raiz mesmo, ou você pode calcular esta raiz com uma calculadora e dar o resultado aproximado
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por R0nny » Sáb Mai 04, 2013 08:02
por R0nny » Sáb Mai 04, 2013 08:02
Mas me diga uma coisa, se voce der o avanço com essa sua raiz(12), no final de toda resoluçao terá que: t=1.1s?
-
R0nny
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Abr 28, 2013 10:53
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Estudante
- Andamento: cursando
 por young_jedi » Sáb Mai 04, 2013 08:49
por young_jedi » Sáb Mai 04, 2013 08:49
nas minhas contas deu 0.84
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por R0nny » Sáb Mai 04, 2013 12:34
por R0nny » Sáb Mai 04, 2013 12:34
A soluçao deve ser 1,1, so que parece que nós os dois nao estamos a chegar la, devemos contactar ao superior ou um moderador para que nos ajude!
-
R0nny
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Abr 28, 2013 10:53
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Estudante
- Andamento: cursando
 por e8group » Sáb Mai 04, 2013 13:54
por e8group » Sáb Mai 04, 2013 13:54
Realmente o discriminante é
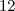
.O colaborador young_jedi estar correto .Mas , apesar de a temperatura ser superior a 10°C quando

,está solução não é única ,afinal de contas trata-se de uma inequação .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por R0nny » Sáb Mai 04, 2013 14:43
por R0nny » Sáb Mai 04, 2013 14:43
Sim Santiago, depois de várias horas de resoluçao deste exercicio eu tambem apanhei o descriminante(delta)=12, éntao aos aplicarmos a outra formula teremos uma raize positiva e negativa, isto é, 1 e acho que é -13.2 se a memória nao me engana, digo várias horas de resoluçao pois estava tentando achar o tal t=1.1, e nao consegui; Como ele nao pode ter um tempo neste caso negativo, obtamos para o t=1. acho que t=1.1s=1

-
R0nny
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Abr 28, 2013 10:53
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Estudante
- Andamento: cursando
 por R0nny » Sáb Mai 04, 2013 14:45
por R0nny » Sáb Mai 04, 2013 14:45
Eu penso que tratando-se de uma inequaçao, se tem o ">", isto quer dizer que admite valores positivos, isto é, acima de 0, como obtemos a nossa raiz(positiva)=1, entao x>1.... 1.1,1.2,1.3...etc...

-
R0nny
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Abr 28, 2013 10:53
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Estudante
- Andamento: cursando
 por e8group » Sáb Mai 04, 2013 15:26
por e8group » Sáb Mai 04, 2013 15:26
A raiz positiva da equação

não é

,o número 1 é uma aproximação por excesso desta raiz .Pela fórmula resolvente , temos
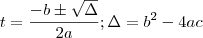
.
Então :
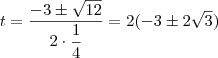
.
Como

,resulta que
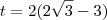
é a raiz da equação
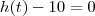
. Como

descreve uma parábola cuja concavidade é voltada para cima ,tem-se necessariamente

para quaisquer

.Desta forma ,sempre que

a temperatura será superior a 10°C .Só acrescentando ,tomando-se

como aproximação para

,vemos que

(nada mau ! De acordo com o wolfram alpha :
http://www.wolframalpha.com/input/?i=2* ... 283%29%29+ )
Editado pela última vez por
e8group em Sáb Mai 04, 2013 15:52, em um total de 1 vez.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por R0nny » Sáb Mai 04, 2013 15:49
por R0nny » Sáb Mai 04, 2013 15:49
Eu havia dito 1 por causa de ao resolver obtive 0.9 entao aproximei por 1

-
R0nny
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Abr 28, 2013 10:53
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Estudante
- Andamento: cursando
 por e8group » Sáb Mai 04, 2013 15:53
por e8group » Sáb Mai 04, 2013 15:53
OK .Observei um erro no texto ,já está editado .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Inequações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinação de divisores
por Abelardo » Seg Mar 07, 2011 00:50
- 4 Respostas
- 3128 Exibições
- Última mensagem por Abelardo

Seg Mar 07, 2011 20:14
Álgebra Elementar
-
- determinação de ponto
por wanderley argenton » Seg Mai 28, 2012 13:58
- 1 Respostas
- 3222 Exibições
- Última mensagem por LuizAquino

Seg Mai 28, 2012 17:42
Geometria Analítica
-
- Determinação de um plano
 por ViniciusAlmeida » Sex Mai 29, 2015 00:07
por ViniciusAlmeida » Sex Mai 29, 2015 00:07
- 0 Respostas
- 1167 Exibições
- Última mensagem por ViniciusAlmeida

Sex Mai 29, 2015 00:07
Geometria Analítica
-
- Determinação de domínio da função
por Jonatan » Qua Jul 28, 2010 13:24
- 1 Respostas
- 3095 Exibições
- Última mensagem por MarceloFantini

Qua Jul 28, 2010 14:51
Funções
-
- demonstração e determinação de raizes
por tigre matematico » Sáb Out 15, 2011 23:29
- 0 Respostas
- 930 Exibições
- Última mensagem por tigre matematico

Sáb Out 15, 2011 23:29
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







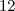 .O colaborador young_jedi estar correto .Mas , apesar de a temperatura ser superior a 10°C quando
.O colaborador young_jedi estar correto .Mas , apesar de a temperatura ser superior a 10°C quando  ,está solução não é única ,afinal de contas trata-se de uma inequação .
,está solução não é única ,afinal de contas trata-se de uma inequação .




 não é
não é  ,o número 1 é uma aproximação por excesso desta raiz .Pela fórmula resolvente , temos
,o número 1 é uma aproximação por excesso desta raiz .Pela fórmula resolvente , temos 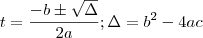 .
. 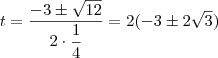 .
.  ,resulta que
,resulta que 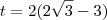 é a raiz da equação
é a raiz da equação 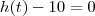 . Como
. Como  descreve uma parábola cuja concavidade é voltada para cima ,tem-se necessariamente
descreve uma parábola cuja concavidade é voltada para cima ,tem-se necessariamente  para quaisquer
para quaisquer  .Desta forma ,sempre que
.Desta forma ,sempre que  a temperatura será superior a 10°C .Só acrescentando ,tomando-se
a temperatura será superior a 10°C .Só acrescentando ,tomando-se  como aproximação para
como aproximação para  ,vemos que
,vemos que  (nada mau ! De acordo com o wolfram alpha : http://www.wolframalpha.com/input/?i=2* ... 283%29%29+ )
(nada mau ! De acordo com o wolfram alpha : http://www.wolframalpha.com/input/?i=2* ... 283%29%29+ )


