Potências

por **Jhennyfer** » Dom Abr 28, 2013 14:15

Oi, desde já peço desculpas... mas não achei nenhum tópico pra colocar a minha questão...
se alguém puder ajuda eu a me localizar melhor, agredeço!

enfim... tenho duas questões e não estou conseguindo resolver.

1)Efetuando as operações indicadas na expressão abaixo, obtemos um número de quatro algarismos . Qual é a soma dos algarismos desse número?
R:7

$(\frac{2^2^0^0^7+2^2^0^0^5}{2^2^0^0^6+2^2^0^0^4}).2006$

Minha primeira tentativa foi tentar dividir primeiro as potencias, e depois somá-las...
mas daí o resultado é 4, e multiplicando por 2006, a soma de algarismos não será 7 =/
- Vi em alguns exemplos que terei que desenvolver a potencia para somar! Mas a potencia é muito grande,
sei que há outra maneira mas não sei qual!
a partir do resultado conclui que o número que resulta das potencias é 2, pois 2x2006=4012 (somando os algarismos obtem-se 7)
Enfim, meu problema está na soma e divisão de potencias.

Questão 2.
(FUVEST-SP) Se...
$4^1^6.5^2^5=\alpha.10^n$
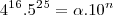
com
$1\leq\alpha<10$
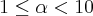
então N é igual a: (no gabarito R:27)

Essa questão nem consegui começar a pensar em algo.

por **Cleyson007** » Seg Abr 29, 2013 11:05

Olá Jhennyfer, bom dia!

Se fosse eu, criaria o tópico em: viewforum.php?f=106

Vou te ajudar com a primeira dúvida. Ok? Acompanhe:

(2^2007 + 2^2005) / (2^2006 + 2^2004) . 2006 =

2^2004(2^3 + 2) / (2^2004(2^2 +1) . 2006 =

10/5 . 2006 =

2 (2006) = 4012

Soma dos algarismos: 4 + 0 + 1 + 2 = 7

Comente qualquer dúvida. Bons estudos :y:

Cleyson007

por **Jhennyfer** » Seg Abr 29, 2013 11:19

Não entendi essa parte :(

2^2004(2^3 + 2) / (2^2004(2^2 +1) . 2006 =

não entendi essa substituição das bases iguais e esse calculo entre parenteses.

por **Cleyson007** » Seg Abr 29, 2013 11:45

Ah sim, vou explicar..

Vou usar o LaTeX para facilitar a visualização:

$\frac{{2}^{2004}({2}^{3}+2)}{{2}^{2004}({2}^{2}+1)}\,.\,2006$

Conhece uma regra da multiplicação onde diz: "Quando as bases são iguais conserva-se a base e soma-se os expoentes"?. Bom, o que eu fiz foi isso!

Primeiro: Coloquei o ${2}^{2004}$ tanto no numerador quanto no denominador para depois "cortar" os dois.

Segundo: Vamos agora aplicar a regra!

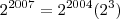${2}^{2007} = {2}^{2004}({2}^{3})}$ --> Conservei a base 2 e somei os expoentes (2004 + 3 = 2007).

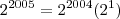${2}^{2005} = {2}^{2004}({2}^{1})}$ --> Conservei a base 2 e somei os expoentes (2004 + 1 = 2005).

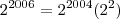${2}^{2006} = {2}^{2004}({2}^{2})}$ --> Conservei a base 2 e somei os expoentes (2004 + 2 = 2006).

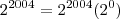${2}^{2004} = {2}^{2004}({2}^{0})}$ --> Conservei a base 2 e somei os expoentes (2004 + 0 = 2004). Aqui vale lembrar que ${2}^{0}=1$ .

Veja se esclareci suas dúvidas. Qualquer coisa estou a disposição :y:

Cleyson007

por **Jhennyfer** » Seg Abr 29, 2013 11:53

Entendi perfeitamente, é que eu ainda não domino muito bem essa parte de simplificar
as potencias, e acabo tendo dúvidas... mas obrigado, me ajudou muito!