 por Jhennyfer » Dom Abr 28, 2013 14:15
por Jhennyfer » Dom Abr 28, 2013 14:15
Oi, desde já peço desculpas... mas não achei nenhum tópico pra colocar a minha questão...
se alguém puder ajuda eu a me localizar melhor, agredeço!
enfim... tenho duas questões e não estou conseguindo resolver.
1)Efetuando as operações indicadas na expressão abaixo, obtemos um número de quatro algarismos . Qual é a soma dos algarismos desse número?
R:7

Minha primeira tentativa foi tentar dividir primeiro as potencias, e depois somá-las...
mas daí o resultado é 4, e multiplicando por 2006, a soma de algarismos não será 7 =/
- Vi em alguns exemplos que terei que desenvolver a potencia para somar! Mas a potencia é muito grande,
sei que há outra maneira mas não sei qual!
a partir do resultado conclui que o número que resulta das potencias é 2, pois 2x2006=4012 (somando os algarismos obtem-se 7)
Enfim, meu problema está na soma e divisão de potencias.
Questão 2.
(FUVEST-SP) Se...
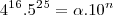
com
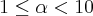
então N é igual a: (no gabarito R:27)
Essa questão nem consegui começar a pensar em algo.
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Seg Abr 29, 2013 11:05
por Cleyson007 » Seg Abr 29, 2013 11:05
Olá Jhennyfer, bom dia!
Se fosse eu, criaria o tópico em:
viewforum.php?f=106Vou te ajudar com a primeira dúvida. Ok? Acompanhe:
(2^2007 + 2^2005) / (2^2006 + 2^2004) . 2006 =
2^2004(2^3 + 2) / (2^2004(2^2 +1) . 2006 =
10/5 . 2006 =
2 (2006) = 4012
Soma dos algarismos: 4 + 0 + 1 + 2 = 7
Comente qualquer dúvida. Bons estudos
 Cleyson007
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Jhennyfer » Seg Abr 29, 2013 11:19
por Jhennyfer » Seg Abr 29, 2013 11:19
Não entendi essa parte :(
2^2004(2^3 + 2) / (2^2004(2^2 +1) . 2006 =
não entendi essa substituição das bases iguais e esse calculo entre parenteses.
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Seg Abr 29, 2013 11:45
por Cleyson007 » Seg Abr 29, 2013 11:45
Ah sim, vou explicar..
Vou usar o LaTeX para facilitar a visualização:

Conhece uma regra da multiplicação onde diz: "Quando as bases são iguais conserva-se a base e soma-se os expoentes"?. Bom, o que eu fiz foi isso!
Primeiro: Coloquei o

tanto no numerador quanto no denominador para depois "cortar" os dois.
Segundo: Vamos agora aplicar a regra!
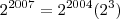
--> Conservei a base 2 e somei os expoentes (2004 + 3 = 2007).
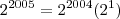
--> Conservei a base 2 e somei os expoentes (2004 + 1 = 2005).
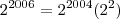
--> Conservei a base 2 e somei os expoentes (2004 + 2 = 2006).
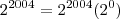
--> Conservei a base 2 e somei os expoentes (2004 + 0 = 2004). Aqui vale lembrar que

.
Veja se esclareci suas dúvidas. Qualquer coisa estou a disposição
 Cleyson007
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Jhennyfer » Seg Abr 29, 2013 11:53
por Jhennyfer » Seg Abr 29, 2013 11:53
Entendi perfeitamente, é que eu ainda não domino muito bem essa parte de simplificar
as potencias, e acabo tendo dúvidas... mas obrigado, me ajudou muito!
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Seg Abr 29, 2013 12:03
por Cleyson007 » Seg Abr 29, 2013 12:03
Ok Jhennyfer!
Fico feliz em saber que pude ajudar

Qualquer coisa estou a disposição..
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Potências...
por Estela » Dom Mai 04, 2008 22:15
- 3 Respostas
- 2580 Exibições
- Última mensagem por Glauber2012

Sex Mar 23, 2012 21:23
Álgebra Elementar
-
- Potências
por Jhennyfer » Qui Mai 16, 2013 11:31
- 3 Respostas
- 2207 Exibições
- Última mensagem por Victor Gabriel

Qui Mai 16, 2013 13:12
Álgebra Elementar
-
- Expressão com potências!
por luizduvidas » Dom Set 25, 2011 01:12
- 1 Respostas
- 1435 Exibições
- Última mensagem por nietzsche

Dom Set 25, 2011 11:27
Álgebra Elementar
-
- Transformação de Potências
por FilipeX » Qua Mar 21, 2012 22:10
- 1 Respostas
- 1941 Exibições
- Última mensagem por joaofonseca

Qua Mar 21, 2012 22:38
Álgebra Elementar
-
- Números Complexos, Potências.
por FrIcaro » Seg Ago 10, 2009 16:11
- 2 Respostas
- 2610 Exibições
- Última mensagem por Elcioschin

Sáb Ago 15, 2009 20:33
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

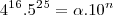
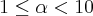






 tanto no numerador quanto no denominador para depois "cortar" os dois.
tanto no numerador quanto no denominador para depois "cortar" os dois. 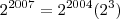 --> Conservei a base 2 e somei os expoentes (2004 + 3 = 2007).
--> Conservei a base 2 e somei os expoentes (2004 + 3 = 2007).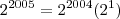 --> Conservei a base 2 e somei os expoentes (2004 + 1 = 2005).
--> Conservei a base 2 e somei os expoentes (2004 + 1 = 2005).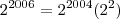 --> Conservei a base 2 e somei os expoentes (2004 + 2 = 2006).
--> Conservei a base 2 e somei os expoentes (2004 + 2 = 2006).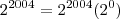 --> Conservei a base 2 e somei os expoentes (2004 + 0 = 2004). Aqui vale lembrar que
--> Conservei a base 2 e somei os expoentes (2004 + 0 = 2004). Aqui vale lembrar que  .
.




