 por JKS » Qui Abr 11, 2013 01:24
por JKS » Qui Abr 11, 2013 01:24
preciso de ajuda,desde já agradeço!
Ache o valor do 25° termo da pg alternante e infinita, sabendo que q =
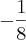
e S=
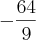
.
GABARITO :

-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Ter Abr 16, 2013 12:15
por DanielFerreira » Ter Abr 16, 2013 12:15
Jks,
bom dia!
Procure expor suas tentativas ao resolver as questões. Fica mais fácil identificar onde 'reside' a dúvida; ou, apenas a resolução é suficiente?
Segue,
Determinemos o primeiro termo da sequência da seguinte forma:

Agora podemos achar o 25° termo.

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por JKS » Dom Abr 21, 2013 18:16
por JKS » Dom Abr 21, 2013 18:16
Muito Obrigada , vou tentar expor minhas tentativas, é porque na resolução das questões feitas por vocês, na maioria das vezes,eu consigo identificar onde foi meu erro,mas quando eu não conseguir eu publico aqui ,mais uma vez te agradeço por me ajudar !!
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Sex Abr 26, 2013 21:30
por DanielFerreira » Sex Abr 26, 2013 21:30
Então tá!

Até a próxima!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sequência alternante PG e PA]
por JKS » Qui Abr 11, 2013 01:45
- 0 Respostas
- 1136 Exibições
- Última mensagem por JKS

Qui Abr 11, 2013 01:45
Progressões
-
- Soma de uma PG infinita
por silvia fillet » Qua Fev 15, 2012 19:53
- 12 Respostas
- 9036 Exibições
- Última mensagem por Rosana Vieira

Qua Fev 22, 2012 17:44
Progressões
-
- [PG infinita e crescente]
por JKS » Qui Abr 11, 2013 01:38
- 1 Respostas
- 2093 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 12:52
Progressões
-
- [PG infinita e crescente]
por JKS » Qui Abr 11, 2013 01:38
- 1 Respostas
- 1885 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 12:49
Progressões
-
- [PG infinita com trigonometria] ITA-SP
por JKS » Qui Abr 11, 2013 01:54
- 1 Respostas
- 2390 Exibições
- Última mensagem por e8group

Qui Abr 11, 2013 13:27
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
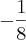 e S=
e S= 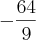 .
.

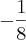 e S=
e S= 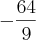 .
.









 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.