 por virginia » Qui Abr 25, 2013 11:21
por virginia » Qui Abr 25, 2013 11:21
A minha resposta não está batendo com o livro me ajudem.
Se f(x):

sendo f(

) a minha resposta desse deu

e a do livro está
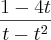
e f(

) a minha resposta deu
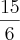
e a do livro

Gostaria de saber onde eu errei.
-
virginia
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 12, 2012 15:15
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
 por DanielFerreira » Qui Abr 25, 2013 17:45
por DanielFerreira » Qui Abr 25, 2013 17:45
Virgínia,
fica difícil encontrar o erro, pois não postou o desenvolvimento de suas contas!
Vou ajudar-te com a primeira, mas, caso não consiga a outra retorne com as contas, ok?!
Segue,
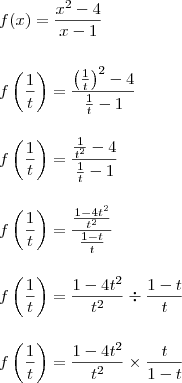
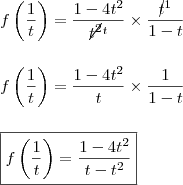
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por virginia » Sex Abr 26, 2013 13:27
por virginia » Sex Abr 26, 2013 13:27
Boa tarde, então a resposta do livro está errada não é, pois a minha resposta deu exatamente essa conforme. Já a segunda segue o desenvolvimento abaixo.




resposta deu 15 sobre 6 e a do livro é 15 sobre 2. Não soube colocar corretamente as fórmulas mais acredito que dá para entender.
Att,
Virginia
-
virginia
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 12, 2012 15:15
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
 por DanielFerreira » Sex Abr 26, 2013 20:17
por DanielFerreira » Sex Abr 26, 2013 20:17
Virgínia,
há um equívoco! Sua resposta estaria correta se fosse
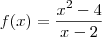
.
Note que o denominador não é o mesmo!
Nessa, a resposta do livro está correta!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por virginia » Sáb Abr 27, 2013 01:17
por virginia » Sáb Abr 27, 2013 01:17
Obrigada.
danjr5 escreveu:Virgínia,
há um equívoco! Sua resposta estaria correta se fosse
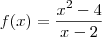
.
Note que o denominador não é o mesmo!
Nessa, a resposta do livro está correta!
-
virginia
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 12, 2012 15:15
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 3251 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2886 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- [Dominio] Cálculo 2- Domínio
por Saturnino Nataniel » Seg Fev 25, 2013 14:09
- 2 Respostas
- 1722 Exibições
- Última mensagem por timoteo

Ter Abr 09, 2013 12:00
Cálculo: Limites, Derivadas e Integrais
-
- DOMÍNIO.
por Matpas » Ter Set 22, 2015 10:27
- 2 Respostas
- 1545 Exibições
- Última mensagem por Matpas

Ter Out 06, 2015 10:04
Funções
-
- [domínio] Funcões
por Cleyson007 » Qua Out 29, 2008 00:28
- 2 Respostas
- 2368 Exibições
- Última mensagem por Cleyson007

Seg Jun 01, 2009 12:38
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 ) a minha resposta desse deu
) a minha resposta desse deu  e a do livro está
e a do livro está 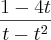
 ) a minha resposta deu
) a minha resposta deu 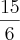 e a do livro
e a do livro 


 ) a minha resposta desse deu
) a minha resposta desse deu  e a do livro está
e a do livro está 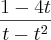
 ) a minha resposta deu
) a minha resposta deu 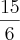 e a do livro
e a do livro 

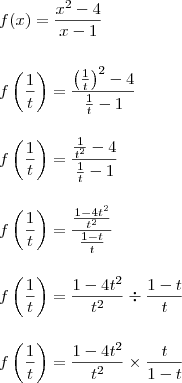







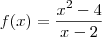 .
. 
.


 .
.



