 por Lenin » Qua Abr 10, 2013 23:36
por Lenin » Qua Abr 10, 2013 23:36
(UEFS) As retas r e s, na figura, são paralelas e o ponto P, vértice do ângulo reto do triângulo PRS, está a
![3\sqrt[2]{3} 3\sqrt[2]{3}](/latexrender/pictures/1268a8c6829b64ebd246f684bce03c50.png)
unidades de distância da reta r e a 4 unidades de distância da reta s.
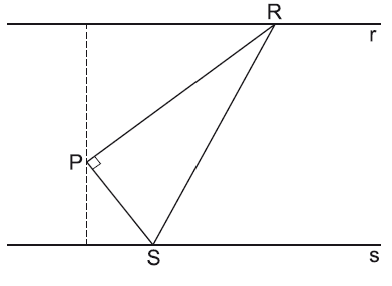
Se a área do triângulo PRS mede 24u.a. então o seu perímetro mede, em unidades de comprimento,
a) 6
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
b)18 + 3
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
c) 24
d) 18 +
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
e) 28
Estou com problemas ao desenvolver esta questão, gostaria de uma ajudinha...
Editado pela última vez por
Lenin em Sex Abr 12, 2013 22:16, em um total de 1 vez.
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por young_jedi » Qui Abr 11, 2013 14:58
por young_jedi » Qui Abr 11, 2013 14:58
voce não colocou a distancia entre P e a reta r
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Lenin » Qui Abr 11, 2013 20:00
por Lenin » Qui Abr 11, 2013 20:00
young_jedi escreveu:voce não colocou a distancia entre P e a reta r
o brother eu coloquei, mas fiquei perdido com essa questão mesmo assim..
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por young_jedi » Qui Abr 11, 2013 20:08
por young_jedi » Qui Abr 11, 2013 20:08
No enunciado tem a distancia da reta s ate o ponto P que 4 porem não tem a distancia da reta r ate o ponto P,
sem este valor não da pra calcular
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Lenin » Sex Abr 12, 2013 21:59
por Lenin » Sex Abr 12, 2013 21:59
young_jedi escreveu:No enunciado tem a distancia da reta s ate o ponto P que 4 porem não tem a distancia da reta r ate o ponto P,
sem este valor não da pra calcular
a brother faltou um dado na questão..
"...vértice do ângulo reto do triângulo PRS, está a
![3\sqrt[2]{3} 3\sqrt[2]{3}](/latexrender/pictures/1268a8c6829b64ebd246f684bce03c50.png)
unidades de distância da reta r e a 4 unidades de distância da reta s.
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por young_jedi » Sex Abr 12, 2013 22:47
por young_jedi » Sex Abr 12, 2013 22:47
era isto mesmo que eu queria saber
voce pode utilizar semelhação de triangulos com os dois triangulos que tem catetos sobre a reta pontilhada, os lados que voce não conhece pode dizer que são a e b então

então podemos formar um trapezio com os tres triangulos, sendo que a area do trapezio sera

mais sabemos que a area do trapezio é igual a soma das areas dos tres triangulos então

igualando as duas equações nos temos
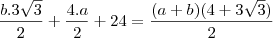
então resolvendo chegamo em
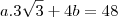
substituindo a da primeira relação que nos encontramos temos


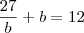


resolvendo encontramos
b=3 ou b=9
para b igual a 9
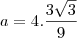

então eccontrando as hipotenusas dos dois triangulos
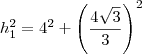

a outra hipotenusa sera
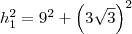

mais as duas hipotenusas dos dois triagnulos são os catetos do triangulo PRS então é so encontrar sua hipotenusa e depois achar o perimtro
comente se tiver duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Lenin » Sex Abr 12, 2013 23:58
por Lenin » Sex Abr 12, 2013 23:58
young_jedi escreveu:era isto mesmo que eu queria saber
voce pode utilizar semelhação de triangulos com os dois triangulos que tem catetos sobre a reta pontilhada, os lados que voce não conhece pode dizer que são a e b então

então podemos formar um trapezio com os tres triangulos, sendo que a area do trapezio sera

mais sabemos que a area do trapezio é igual a soma das areas dos tres triangulos então

igualando as duas equações nos temos
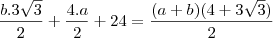
então resolvendo chegamo em
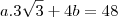
substituindo a da primeira relação que nos encontramos temos


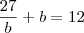


resolvendo encontramos
b=3 ou b=9
para b igual a 9
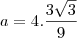

então eccontrando as hipotenusas dos dois triangulos
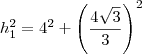

a outra hipotenusa sera
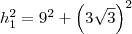

mais as duas hipotenusas dos dois triagnulos são os catetos do triangulo PRS então é so encontrar sua hipotenusa e depois achar o perimtro
comente se tiver duvidas
olha eu achei que a Hipotenusa do triangulo PSR é
![\sqrt[]{172} \sqrt[]{172}](/latexrender/pictures/4cf2add66a10daec69ace7c207687dde.png)
logo eu achei que isso é
![2\sqrt[]{43} 2\sqrt[]{43}](/latexrender/pictures/4f5c4608479f8f8408f109a538456561.png)
e uso a fórmula de perímetro que é:
![P = 6\sqrt[]{3} + 2\sqrt[]{43} + 8 P = 6\sqrt[]{3} + 2\sqrt[]{43} + 8](/latexrender/pictures/b1b0cfd6fd2733748c717f77e77fd4d3.png)
só que não dá a resposta certa, que é a letra C) 24.. =\
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por young_jedi » Sáb Abr 13, 2013 00:12
por young_jedi » Sáb Abr 13, 2013 00:12
lembra que na equação de baskara encontramos dois valores para b
3 e 9
fazendo com b=3 chega-se a resposta
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Lenin » Sáb Abr 13, 2013 11:03
por Lenin » Sáb Abr 13, 2013 11:03
young_jedi escreveu:lembra que na equação de baskara encontramos dois valores para b
3 e 9
fazendo com b=3 chega-se a resposta
A brother, vc inverteu os valores..do ponto P à reta s mede

e da reta r ao ponto P mede
![3\sqrt[]{3} 3\sqrt[]{3}](/latexrender/pictures/8f02447859000765689bdee72a9b79b7.png)
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por young_jedi » Sáb Abr 13, 2013 13:04
por young_jedi » Sáb Abr 13, 2013 13:04
não inverti, é isso mesmo, como a equação tem duas raizes voce tem que fazer o calculo para as duas raizes
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Lenin » Sáb Abr 13, 2013 19:31
por Lenin » Sáb Abr 13, 2013 19:31
young_jedi escreveu:não inverti, é isso mesmo, como a equação tem duas raizes voce tem que fazer o calculo para as duas raizes
A cara, consegui, vlw..hehe
uma questão dessa em um vestibular tinha chutado..pq com esse calculo todo que deu uma pagina inteira mais um pedaço do verso..haushasuhas
abraços
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo do Perímetro no quadrilátero
 por Lana Brasil » Qui Mai 30, 2013 18:10
por Lana Brasil » Qui Mai 30, 2013 18:10
- 2 Respostas
- 3478 Exibições
- Última mensagem por Lana Brasil

Sex Mai 31, 2013 15:19
Geometria Plana
-
- Calculo de perimetro do triangulo retangulo
por Marcinha » Dom Nov 13, 2011 16:12
- 1 Respostas
- 2967 Exibições
- Última mensagem por Andreza

Dom Nov 13, 2011 18:08
Geometria Plana
-
- cálculo de perímetro envolvendo números irracionais
por jose henrique » Qua Fev 16, 2011 16:42
- 5 Respostas
- 3615 Exibições
- Última mensagem por jose henrique

Qui Fev 17, 2011 10:25
Álgebra Elementar
-
- perímetro
 por GeRmE » Seg Nov 15, 2010 13:05
por GeRmE » Seg Nov 15, 2010 13:05
- 2 Respostas
- 1979 Exibições
- Última mensagem por GeRmE

Seg Nov 15, 2010 15:51
Geometria Plana
-
- Perimetro
por Robinho » Sáb Jan 14, 2012 14:41
- 2 Respostas
- 1639 Exibições
- Última mensagem por Robinho

Sáb Jan 14, 2012 14:55
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![3\sqrt[2]{3} 3\sqrt[2]{3}](/latexrender/pictures/1268a8c6829b64ebd246f684bce03c50.png) unidades de distância da reta r e a 4 unidades de distância da reta s.
unidades de distância da reta r e a 4 unidades de distância da reta s.
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)






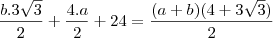
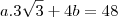


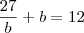


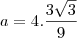

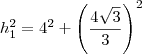

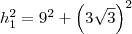

![\sqrt[]{172} \sqrt[]{172}](/latexrender/pictures/4cf2add66a10daec69ace7c207687dde.png) logo eu achei que isso é
logo eu achei que isso é ![2\sqrt[]{43} 2\sqrt[]{43}](/latexrender/pictures/4f5c4608479f8f8408f109a538456561.png) e uso a fórmula de perímetro que é:
e uso a fórmula de perímetro que é:![P = 6\sqrt[]{3} + 2\sqrt[]{43} + 8 P = 6\sqrt[]{3} + 2\sqrt[]{43} + 8](/latexrender/pictures/b1b0cfd6fd2733748c717f77e77fd4d3.png)
 e da reta r ao ponto P mede
e da reta r ao ponto P mede ![3\sqrt[]{3} 3\sqrt[]{3}](/latexrender/pictures/8f02447859000765689bdee72a9b79b7.png)