era isto mesmo que eu queria saber
voce pode utilizar semelhação de triangulos com os dois triangulos que tem catetos sobre a reta pontilhada, os lados que voce não conhece pode dizer que são a e b então

então podemos formar um trapezio com os tres triangulos, sendo que a area do trapezio sera

mais sabemos que a area do trapezio é igual a soma das areas dos tres triangulos então

igualando as duas equações nos temos
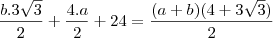
então resolvendo chegamo em
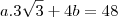
substituindo a da primeira relação que nos encontramos temos


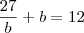


resolvendo encontramos
b=3 ou b=9
para b igual a 9
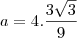

então eccontrando as hipotenusas dos dois triangulos
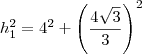

a outra hipotenusa sera
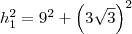

mais as duas hipotenusas dos dois triagnulos são os catetos do triangulo PRS então é so encontrar sua hipotenusa e depois achar o perimtro
comente se tiver duvidas
![3\sqrt[2]{3} 3\sqrt[2]{3}](/latexrender/pictures/1268a8c6829b64ebd246f684bce03c50.png) unidades de distância da reta r e a 4 unidades de distância da reta s.
unidades de distância da reta r e a 4 unidades de distância da reta s.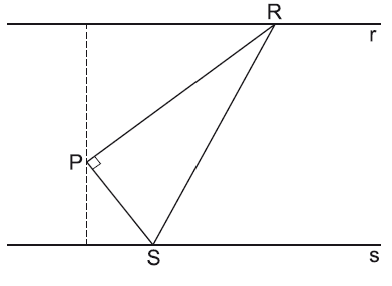
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)






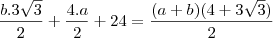
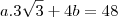


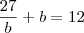


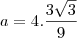

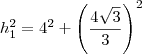

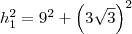

![\sqrt[]{172} \sqrt[]{172}](/latexrender/pictures/4cf2add66a10daec69ace7c207687dde.png) logo eu achei que isso é
logo eu achei que isso é ![2\sqrt[]{43} 2\sqrt[]{43}](/latexrender/pictures/4f5c4608479f8f8408f109a538456561.png) e uso a fórmula de perímetro que é:
e uso a fórmula de perímetro que é:![P = 6\sqrt[]{3} + 2\sqrt[]{43} + 8 P = 6\sqrt[]{3} + 2\sqrt[]{43} + 8](/latexrender/pictures/b1b0cfd6fd2733748c717f77e77fd4d3.png)
 e da reta r ao ponto P mede
e da reta r ao ponto P mede ![3\sqrt[]{3} 3\sqrt[]{3}](/latexrender/pictures/8f02447859000765689bdee72a9b79b7.png)

 .
.



