 por Matheus Lacombe O » Sáb Mar 30, 2013 18:25
por Matheus Lacombe O » Sáb Mar 30, 2013 18:25
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por Russman » Sáb Mar 30, 2013 19:24
por Russman » Sáb Mar 30, 2013 19:24
Tem que dividir o 4 por 2. Não esquece que tem o
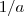
ali na frente da função.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Matheus Lacombe O » Sáb Mar 30, 2013 20:19
por Matheus Lacombe O » Sáb Mar 30, 2013 20:19
Bá, não entendi , não.. Olha: o "x" não é igual a 2 e o "a" não é igual a "x" e a fórmula não é:

substituindo na fórmula, não dá:
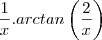
??
Pelo amor de Deus, socorro! Preciso entender isso. É muito importante!
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por Russman » Dom Mar 31, 2013 12:33
por Russman » Dom Mar 31, 2013 12:33
O

é a variável de integração!! Assim, você não pode tomar um valor específico para

. Note que

. Portanto, você tem de tomar
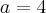
e não

. A ordem que eles aparecem no denominador não importa:
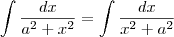
Assim, você tem de tomar em

, em comparação com

,

pois

. Entende onde você está se confundindo?
Lembre-se que a ordem das parcelas não altera a soma:

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Matheus Lacombe O » Dom Mar 31, 2013 21:15
por Matheus Lacombe O » Dom Mar 31, 2013 21:15
-Tá, legal. Eu consegui resolver pelo que você me explicou. Mas sem querer abusar..
-Eu pensei o seguinte: E se a minha integral não estivesse "prontinha" para aplicar na fórmula? E se ao invés de

eu tivesse

, por exemplo? Você disse que eu não posso comparar o "

" com um valor específico, 4(quatro) no caso, então aqui eu teria que comparar

com

e

com

?
-Seria isso?
-Mais uma vez, obrigado pela atenção e dedicação.
Att. Matheus L. Oliveira
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por Russman » Dom Mar 31, 2013 21:19
por Russman » Dom Mar 31, 2013 21:19
Não. A sua fórmula aplica-se somente a integral

. No caso de

teríamos de estudar e desenvolver outra relação.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- fórmula
por Ismafa » Ter Fev 17, 2009 01:29
- 2 Respostas
- 3228 Exibições
- Última mensagem por Ismafa

Qua Fev 25, 2009 09:57
Sistemas de Equações
-
- Fórmula de PMT
por Leonardonc » Seg Ago 27, 2012 09:27
- 0 Respostas
- 2278 Exibições
- Última mensagem por Leonardonc

Seg Ago 27, 2012 09:27
Matemática Financeira
-
- demonstração de fórmula
 por Troe » Ter Out 20, 2009 18:07
por Troe » Ter Out 20, 2009 18:07
- 0 Respostas
- 2172 Exibições
- Última mensagem por Troe

Ter Out 20, 2009 18:07
Trigonometria
-
- Qual é a fórmula?
por thales7l » Qua Nov 04, 2009 18:02
- 1 Respostas
- 2224 Exibições
- Última mensagem por Neperiano

Dom Set 18, 2011 13:53
Estatística
-
- duvida da formula
por pavaroti » Sáb Jan 02, 2010 05:07
- 7 Respostas
- 5895 Exibições
- Última mensagem por Molina

Sáb Jan 02, 2010 22:40
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





![x=\sqrt[]{4} x=\sqrt[]{4}](/latexrender/pictures/42e8fbd472e318e596f0638a896e5e36.png)




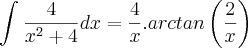






![x=\sqrt[]{4} x=\sqrt[]{4}](/latexrender/pictures/42e8fbd472e318e596f0638a896e5e36.png)




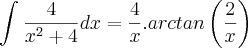

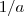 ali na frente da função.
ali na frente da função.

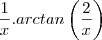

 é a variável de integração!! Assim, você não pode tomar um valor específico para
é a variável de integração!! Assim, você não pode tomar um valor específico para  . Note que
. Note que  . Portanto, você tem de tomar
. Portanto, você tem de tomar 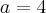 e não
e não  . A ordem que eles aparecem no denominador não importa:
. A ordem que eles aparecem no denominador não importa: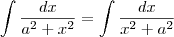
 , em comparação com
, em comparação com  ,
,  pois
pois  . Entende onde você está se confundindo?
. Entende onde você está se confundindo? .
.
 eu tivesse
eu tivesse  , por exemplo? Você disse que eu não posso comparar o "
, por exemplo? Você disse que eu não posso comparar o " " com um valor específico, 4(quatro) no caso, então aqui eu teria que comparar
" com um valor específico, 4(quatro) no caso, então aqui eu teria que comparar  com
com  e
e  com
com  ?
?
 . No caso de
. No caso de  teríamos de estudar e desenvolver outra relação.
teríamos de estudar e desenvolver outra relação.