Ajuda com questão envolvendo fração

por **Jovilaco** » Dom Mar 24, 2013 19:15

Eu emperrei neste exercício que o professor passou na lista, eu não me lembro direito o que faço pra resolver... acho o MMC passou pela minha cabeça... não me lembro se existia alguma propriedade de inequações que me ajudasse a resolver este exercício. Obrigado.

Se vocês conseguirem me mostrar passo a passo eu agradeço imensamente.

1/(x+1)<2/(3x-1)

por **DanielFerreira** » Dom Mar 24, 2013 19:35

Olá Jovilaco,
boa noite!

$\\ \frac{1}{x + 1} < \frac{2}{3x - 1} \\\\\\ \frac{1}{x + 1} - \frac{2}{3x - 1} < 0 \\\\\\ \frac{1 \cdot (3x - 1) - 2(x + 1)}{(x + 1)(3x - 1)} < 0 \\\\\\ \frac{3x - 1 - 2x - 2}{(x + 1)(3x - 1)} < 0 \\\\\\ \frac{x - 3}{(x + 1)(3x - 1)} < 0$

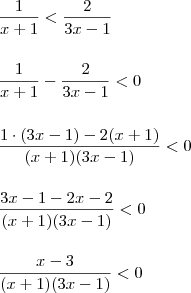
Tente concluir, caso contrário, retorne!

Att,

Daniel.

por **Jovilaco** » Dom Mar 24, 2013 22:07

Nossa... eu tava tentando multiplicar em x.... -_-
Pq o sinal da igualdade não se inverteu ao multiplicarmos a incognita pelo negativo?

por **DanielFerreira** » Sex Mar 29, 2013 01:04

Jovilaco,
desculpe-me pela demora!
Não inverti o sinal da desigualdade por que não multipliquei a incógnita pelo negativo.
Vale lembrar que, do lado direito da desigualdade devemos ter apenas o zero (bem como fiz na segunda linha da 'resolução').