 por Douglas16 » Dom Mar 10, 2013 17:24
por Douglas16 » Dom Mar 10, 2013 17:24
Determine as constantes a, b, e c de tal forma que satisfaçam a seguinte relação.
![\lim_{x\rightarrow0} \frac{\sqrt[]{1+x}-\left(1+a*x+b*x*x \right)}{x*x*x}=c \lim_{x\rightarrow0} \frac{\sqrt[]{1+x}-\left(1+a*x+b*x*x \right)}{x*x*x}=c](/latexrender/pictures/9e2431bf4f4217ae0714cec12188140c.png)
Baseando no fato de que x se aproxima de zero o denominador fica cada vez menor, o que torna o valor do numerador (quando se divide o numerador pelo denominador) cada vez maior e, como o numerador pode ser tanto negativo quanto positivo, minha conclusão (se não esqueci mais detalhes), é:
c= infinito negativo ou infinito positivo e a pertence aos reais e b pertence aos reais.
Será que é lógico e correto o que fiz?
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Dom Mar 10, 2013 23:57
por young_jedi » Dom Mar 10, 2013 23:57
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Douglas16 » Seg Mar 11, 2013 10:10
por Douglas16 » Seg Mar 11, 2013 10:10
Muito bem.
Como o exercício não define se a constante c é um valor finito e nem um valor infinito, fica a questão. Considerando c como um valor finito, sua resposta é a correta, mas se c é um valor infinito, penso (se estiver errado corrijam-me) que a resposta do primeiro post é uma alternativa.
Ou o exercício dá as condições necessárias para definir c como um valor finito?
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Seg Mar 11, 2013 11:27
por young_jedi » Seg Mar 11, 2013 11:27
no enunciado ele pede para definir as constantes a, b e c
se c é uma constante podemos assumir que ele é um valor numerico finito.
o enunciado realmente deixou meio vago, mais eu acho que essa é a melhor interpretação
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Douglas16 » Seg Mar 11, 2013 11:51
por Douglas16 » Seg Mar 11, 2013 11:51
Sabe o que acontece?
No material didático, em outros exercícios, o enunciado diz: "Calcule os seguintes valores limites" e, tipo, em muitos limites o valor encontrado é infinito positivo ou infinito negativo, mas nestes casos o limite não existe, pois é ilógico considerar o infinito positivo ou infinito negativo como um limite de uma expressão, e isso eu já sabia faz tempo. Mas como em todo começo de exercício tem o tal do enunciado citado anteriormente, passa o tempo e esqueço essa particularidade. Então no meu ponto de vista o erro provém também da forma do enunciado, que induz ao esquecimento desta particularidade, aí quando se tem um exercício como esse, ocorre uma má interpretação das condições dadas para resolver o exercício, aí já viu, vira uma bolinha de neve e kabum!!! Resultado: erro.
Cada coisa, hein...
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Douglas16 » Seg Mar 11, 2013 12:07
por Douglas16 » Seg Mar 11, 2013 12:07
Bem que o enunciado está correto, o que está errado é minha má interpretação.
Como você disse, o enunciado diz que a, b e c são valores constantes, logo não podem ser valores infinitos.
Resolvi o meu erro de interpretação?
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Seg Mar 11, 2013 14:04
por young_jedi » Seg Mar 11, 2013 14:04
é isso mesmo
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Adição de Polinômios minha resposta diferente da do livro
por ravi » Ter Jan 31, 2012 14:02
- 2 Respostas
- 2248 Exibições
- Última mensagem por Arkanus Darondra

Ter Jan 31, 2012 14:49
Polinômios
-
- [Função 2º grau] Minha resposta está certa?
por Richard Oliveira » Sex Mai 04, 2012 03:05
- 1 Respostas
- 1719 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 00:06
Funções
-
- Quero saber se minha resposta está correta
por Raquel299 » Seg Mar 09, 2015 09:53
- 3 Respostas
- 2737 Exibições
- Última mensagem por Raquel299

Sex Abr 10, 2015 10:49
Funções
-
- [Métodos de Contagem] minha resposta não "bateu" !
por Guto150 » Sex Ago 29, 2014 15:19
- 3 Respostas
- 5764 Exibições
- Última mensagem por young_jedi

Sáb Ago 30, 2014 15:53
Binômio de Newton
-
- Exercicos da minha apostila
por Guilherme35 » Qui Set 20, 2012 15:11
- 1 Respostas
- 2907 Exibições
- Última mensagem por LuizAquino

Qui Set 20, 2012 15:52
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow0} \frac{\sqrt[]{1+x}-\left(1+a*x+b*x*x \right)}{x*x*x}=c \lim_{x\rightarrow0} \frac{\sqrt[]{1+x}-\left(1+a*x+b*x*x \right)}{x*x*x}=c](/latexrender/pictures/9e2431bf4f4217ae0714cec12188140c.png)



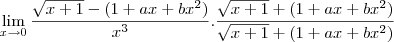


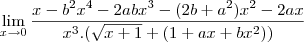
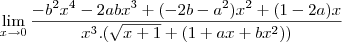
 do denominador com o numerador, mais para isso é necessario que todos os expoentes de x do numerador seja maiores ou iguais a 3 portanto
do denominador com o numerador, mais para isso é necessario que todos os expoentes de x do numerador seja maiores ou iguais a 3 portanto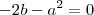
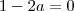
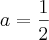


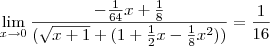



 , avisa que eu resolvo.
, avisa que eu resolvo.

