 por Douglas16 » Seg Mar 11, 2013 11:51
por Douglas16 » Seg Mar 11, 2013 11:51
Sabe o que acontece?
No material didático, em outros exercícios, o enunciado diz: "Calcule os seguintes valores limites" e, tipo, em muitos limites o valor encontrado é infinito positivo ou infinito negativo, mas nestes casos o limite não existe, pois é ilógico considerar o infinito positivo ou infinito negativo como um limite de uma expressão, e isso eu já sabia faz tempo. Mas como em todo começo de exercício tem o tal do enunciado citado anteriormente, passa o tempo e esqueço essa particularidade. Então no meu ponto de vista o erro provém também da forma do enunciado, que induz ao esquecimento desta particularidade, aí quando se tem um exercício como esse, ocorre uma má interpretação das condições dadas para resolver o exercício, aí já viu, vira uma bolinha de neve e kabum!!! Resultado: erro.
Cada coisa, hein...
![\lim_{x\rightarrow0} \frac{\sqrt[]{1+x}-\left(1+a*x+b*x*x \right)}{x*x*x}=c \lim_{x\rightarrow0} \frac{\sqrt[]{1+x}-\left(1+a*x+b*x*x \right)}{x*x*x}=c](/latexrender/pictures/9e2431bf4f4217ae0714cec12188140c.png)



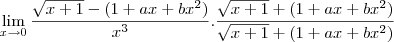


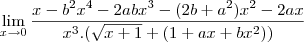
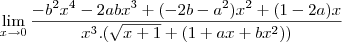
 do denominador com o numerador, mais para isso é necessario que todos os expoentes de x do numerador seja maiores ou iguais a 3 portanto
do denominador com o numerador, mais para isso é necessario que todos os expoentes de x do numerador seja maiores ou iguais a 3 portanto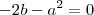
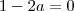
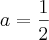


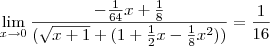


 .
.
 :
: