Enunciado: Prove que, dado um número racional
 e um número natural
e um número natural  , nem sempre
, nem sempre ![\sqrt[n]{\frac{a}{b}} \sqrt[n]{\frac{a}{b}}](/latexrender/pictures/317d53501ad6cd19416e2938df2defda.png) é racional.
é racional.minha resolução não foi baseada totalmente em contas.
Resolução: Considerando
 uma fração irredutível e sabendo que
uma fração irredutível e sabendo que ![\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}](/latexrender/pictures/7a922c3446debb68c0d058dbbdbc1a74.png) , claramente
, claramente ![\sqrt[n]{a} \sqrt[n]{a}](/latexrender/pictures/bf7ff33f3b129b15c06203d60f007807.png) ou
ou ![\sqrt[n]{b} \sqrt[n]{b}](/latexrender/pictures/d6cc5502569af8ca13b9a696cb5d070a.png) será irracional, porque como o MDC(a,b)= 1 e dessa forma a ou b será primo,tirando a raiz de a e b, uma delas será irracional. Então, o quociente de um númerou racional por um número irracional, não importando a ordem, resultara num número irracional.
será irracional, porque como o MDC(a,b)= 1 e dessa forma a ou b será primo,tirando a raiz de a e b, uma delas será irracional. Então, o quociente de um númerou racional por um número irracional, não importando a ordem, resultara num número irracional.Minha resolução esta certa??


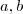 não primos com
não primos com  não múltiplo de
não múltiplo de  ,ou seja ,
,ou seja , 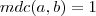 e além disso se
e além disso se 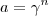 e
e 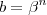 para
para  e
e  naturais ,nestas condições ,
naturais ,nestas condições ,![\sqrt[n]{ \frac{a}{b} } \sqrt[n]{ \frac{a}{b} }](/latexrender/pictures/00c8df4ccccd8ca8b42c72f26800a6e6.png) é racional .Conclusão
é racional .Conclusão 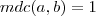 não implica que
não implica que  e fixado
e fixado 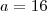 e
e  .
.  não são primos pois
não são primos pois 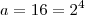 e
e 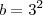 .
. ![\sqrt[n]{ \frac{a}{b} }= \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \frac{2^2}{3} \sqrt[n]{ \frac{a}{b} }= \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \frac{2^2}{3}](/latexrender/pictures/2908f50efa424c3bc9fc97afa0da1631.png)

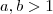 são naturais
são naturais  existem primos positivos
existem primos positivos 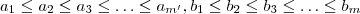 ,tais que se
,tais que se  não são primos , eles podem ser escritos da seguinte forma :
não são primos , eles podem ser escritos da seguinte forma : 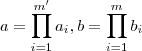 .
. 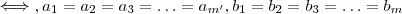 e
e 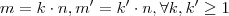 . (**) Caso contrário não é racional .
. (**) Caso contrário não é racional .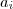 e
e 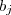 não simultaneamente iguais para
não simultaneamente iguais para 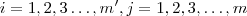 .
.  .
. ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)