Abaixo segue duas expressões modelo:
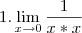
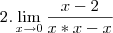

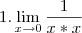
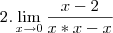

 e desejamos estudar o que acontece com ela em dado
e desejamos estudar o que acontece com ela em dado  . Assim, calculamos o limite
. Assim, calculamos o limite  . Se este limite existir, isto é, se existe um VALOR REAL
. Se este limite existir, isto é, se existe um VALOR REAL  tal que
tal que 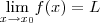 então dizemos que esta função é limitada por
então dizemos que esta função é limitada por  em
em  . Porém, se
. Porém, se 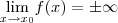 então dizemos que a função não é limitada, ou seja, o limite em
então dizemos que a função não é limitada, ou seja, o limite em  não existe.
não existe.  de
de  pela esquerda e pela direita. Por exemplo, dizer que
pela esquerda e pela direita. Por exemplo, dizer que 
 de
de  vindo DA DIREITA pela função
vindo DA DIREITA pela função 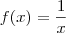 estamos tendo valores cada vez maiores. Agora, se aproximarmos
estamos tendo valores cada vez maiores. Agora, se aproximarmos  peka esquerda nessa função teremos não mais
peka esquerda nessa função teremos não mais  e sim
e sim 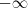 . De fato,
. De fato,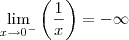



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes