 por Rafael16 » Seg Jan 14, 2013 20:02
por Rafael16 » Seg Jan 14, 2013 20:02
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Russman » Seg Jan 14, 2013 20:28
por Russman » Seg Jan 14, 2013 20:28
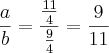
Dois comentários:
1°) Se você supõe que a fração é

então, necessariamente, os números

e

devem ser INTEIROS de forma que a sua subtração, isto é,

, deve ser inteira também. Logo, o resultado

é ,claramente, errado.
2°) Você partiu de
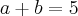
e, no final, calculou um resultado

. É verdade que

?
É sempre bom conferir o resultado encontrado com a previsão inicial.
Você está no caminho certo. Apenas refaça a manipulação de
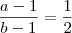
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Rafael16 » Seg Jan 14, 2013 20:55
por Rafael16 » Seg Jan 14, 2013 20:55
Aaaaassimm entendi!
É só fazer isso né?
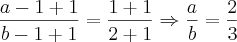
Obrigado Russman!
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Russman » Seg Jan 14, 2013 21:14
por Russman » Seg Jan 14, 2013 21:14
Não, você não pode fazer isso!
Se você somar

, por exemplo, em

,que é o numerador da fração, você está, na verdade, somando

a

.

.
Um exemplo pra te mostrar que isso que você fez deu certo por uma coincidência.

Claramente isto não está certo!
Você pensou antes bem. Tome
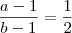
de forma que

A última relação é a que você deve juntar a
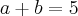
e resolver o sistema

.
Aí sim, a solução é

e

.
Conferindo:
 OK!
OK!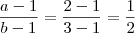 OK!
OK!"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Rafael16 » Seg Jan 14, 2013 21:26
por Rafael16 » Seg Jan 14, 2013 21:26
Ah sim.
Valeu Russman pelas dicas de como "pensar matematicamente" hehe.
Matemática é f*** mesmo...
Se eu fizesse física igual você, eu ia ficar doido e desistir logo no primeiro semestre. rsrs
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Russman » Seg Jan 14, 2013 21:30
por Russman » Seg Jan 14, 2013 21:30
HAHAHA
Pra se sair bem em Matemática você deve fazer bastante exercícios! O nome mesmo já diz: exercitar. Ou seja, é como um treinamento. Concordo que ela exija bastante prática. Com o tempo você vai pegando o jeito e é até capaz de gostar, pq Matemática é uma ciência brilhante.
Bons estudos!

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistemas Lineares] Problema
por vanessafey » Qui Set 22, 2011 15:15
- 2 Respostas
- 3464 Exibições
- Última mensagem por Henriqueitu

Qui Out 06, 2011 15:14
Sistemas de Equações
-
- [Problema de Aritmética - Sistemas] Não sei para onde vai.
por Leocondeuba » Dom Mai 19, 2013 22:44
- 2 Respostas
- 3210 Exibições
- Última mensagem por Leocondeuba

Seg Mai 20, 2013 13:10
Aritmética
-
- Sistemas de equação.
por 380625 » Sex Mar 25, 2011 18:17
- 1 Respostas
- 1195 Exibições
- Última mensagem por LuizAquino

Sex Mar 25, 2011 18:29
Sistemas de Equações
-
- Sistemas de equação.
por 380625 » Qua Abr 06, 2011 16:31
- 1 Respostas
- 1833 Exibições
- Última mensagem por Elcioschin

Qua Abr 06, 2011 18:11
Sistemas de Equações
-
- Problemas de equação e sistemas de 1º grau
por gigante2010 » Dom Out 17, 2010 15:22
- 3 Respostas
- 4216 Exibições
- Última mensagem por MarceloFantini

Dom Out 17, 2010 23:00
Tópicos sem Interação (leia as regras)
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
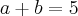




 e
e 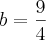


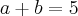




 e
e 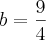



 então, necessariamente, os números
então, necessariamente, os números  e
e  devem ser INTEIROS de forma que a sua subtração, isto é,
devem ser INTEIROS de forma que a sua subtração, isto é,  , deve ser inteira também. Logo, o resultado
, deve ser inteira também. Logo, o resultado  é ,claramente, errado.
é ,claramente, errado.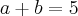 e, no final, calculou um resultado
e, no final, calculou um resultado  . É verdade que
. É verdade que  ?
? 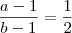 .
.
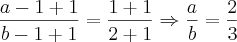

 , por exemplo, em
, por exemplo, em  ,que é o numerador da fração, você está, na verdade, somando
,que é o numerador da fração, você está, na verdade, somando  a
a  .
. .
.
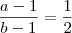

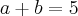 e resolver o sistema
e resolver o sistema  .
. e
e  .
. OK!
OK!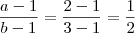 OK!
OK!



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
