Resposta: 2/3
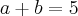

Resolvendo isso chego a



 e
e 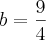
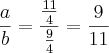


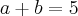




 e
e 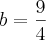



 então, necessariamente, os números
então, necessariamente, os números  e
e  devem ser INTEIROS de forma que a sua subtração, isto é,
devem ser INTEIROS de forma que a sua subtração, isto é,  , deve ser inteira também. Logo, o resultado
, deve ser inteira também. Logo, o resultado  é ,claramente, errado.
é ,claramente, errado.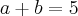 e, no final, calculou um resultado
e, no final, calculou um resultado  . É verdade que
. É verdade que  ?
? 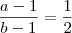 .
.
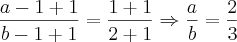

 , por exemplo, em
, por exemplo, em  ,que é o numerador da fração, você está, na verdade, somando
,que é o numerador da fração, você está, na verdade, somando  a
a  .
. .
.
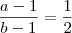

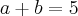 e resolver o sistema
e resolver o sistema  .
. e
e  .
. OK!
OK!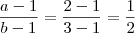 OK!
OK!



Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
