A resposta no livro do Guidorozzi é 0.
Já fiz uma mudança de Variável
![u = {e}^{{x}^{2}} - 1, \Rightarrow x = \sqrt[2]{Ln\left(u+1 \right)} u = {e}^{{x}^{2}} - 1, \Rightarrow x = \sqrt[2]{Ln\left(u+1 \right)}](/latexrender/pictures/afd4b8097237b3778caef9272066b225.png)
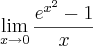 =
= ![\lim_{u\rightarrow0} = \frac{u}{\sqrt[2]{Ln\left(u+1 \right)}} \lim_{u\rightarrow0} = \frac{u}{\sqrt[2]{Ln\left(u+1 \right)}}](/latexrender/pictures/11c9965c82be6e19daa69f909751be08.png)
Eu cheguei um pouco mais longe, mas é complicado por aqui no site...
Se puderem me explicar, Agradeço..


![u = {e}^{{x}^{2}} - 1, \Rightarrow x = \sqrt[2]{Ln\left(u+1 \right)} u = {e}^{{x}^{2}} - 1, \Rightarrow x = \sqrt[2]{Ln\left(u+1 \right)}](/latexrender/pictures/afd4b8097237b3778caef9272066b225.png)
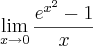 =
= ![\lim_{u\rightarrow0} = \frac{u}{\sqrt[2]{Ln\left(u+1 \right)}} \lim_{u\rightarrow0} = \frac{u}{\sqrt[2]{Ln\left(u+1 \right)}}](/latexrender/pictures/11c9965c82be6e19daa69f909751be08.png)


 . Utilize a propriedade "limite do produto é o produto dos limites " . Além disso , mostre que um destes produtos dos limites é 1(usando o limite fundamental
. Utilize a propriedade "limite do produto é o produto dos limites " . Além disso , mostre que um destes produtos dos limites é 1(usando o limite fundamental  .E , o outro limite resulta zero .
.E , o outro limite resulta zero .
![\frac{u\sqrt[2]{Ln\left(u+1 \right)}}{Ln\left(u+1 \right)} \frac{u\sqrt[2]{Ln\left(u+1 \right)}}{Ln\left(u+1 \right)}](/latexrender/pictures/7db0008f5718d6f34dff69fb3180dc56.png)




Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)