 por brunnoguilherme » Dom Jan 13, 2013 20:04
por brunnoguilherme » Dom Jan 13, 2013 20:04
Use o método de multiplicadores de Lagrange para achar um valor mínimo relativo a função f para a qual
f(x,y,z)=x²+4y²+16z² com o vínculo (a)xyz = 1; (b)xy = 1; (c)x = 1.
-
brunnoguilherme
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Jan 13, 2013 00:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Fisica
- Andamento: cursando
 por Russman » Dom Jan 13, 2013 22:12
por Russman » Dom Jan 13, 2013 22:12
Você só precisa resolver o sistema

onde
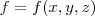
é a função a ser otimizada,
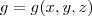
a função de restrição( ou vínculo),

o multiplicador e

o nível da restrição.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo - multiplicadores de Lagrange
por brunnoguilherme » Dom Jan 13, 2013 20:01
- 1 Respostas
- 1466 Exibições
- Última mensagem por timoteo

Dom Jan 13, 2013 23:07
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda em Calculo - multiplicadores de Lagrange
por brunnoguilherme » Dom Jan 13, 2013 00:32
- 1 Respostas
- 2987 Exibições
- Última mensagem por young_jedi

Dom Jan 13, 2013 12:52
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de minimos,máximos usando multiplos de lagrange
por Fernandobertolaccini » Seg Jan 05, 2015 16:39
- 1 Respostas
- 1572 Exibições
- Última mensagem por Russman

Ter Jan 06, 2015 01:13
Cálculo: Limites, Derivadas e Integrais
-
- Multiplicadores de Lagrange
por Zkz » Sex Jun 05, 2009 21:00
- 0 Respostas
- 1894 Exibições
- Última mensagem por Zkz

Sex Jun 05, 2009 21:00
Cálculo: Limites, Derivadas e Integrais
-
- Multiplicadores de Lagrange
por luciamoura » Sex Nov 26, 2010 17:55
- 0 Respostas
- 1734 Exibições
- Última mensagem por luciamoura

Sex Nov 26, 2010 17:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




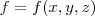 é a função a ser otimizada,
é a função a ser otimizada, 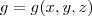 a função de restrição( ou vínculo),
a função de restrição( ou vínculo),  o multiplicador e
o multiplicador e  o nível da restrição.
o nível da restrição.