5. O lucro mensal total de uma empresa obtido na produção e venda de x centenas de termostatos mecânicos e y unidades de termostatos eletrônicos é dado pela função:
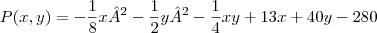
onde
 é o lucro em centenas de reais. Se a produção dos termostatos está condicionada a um total de 4000 unidades por mês, quantas unidades de cada modelo a empresa deveria fabricar para obter o maior lucro possível? Qual é o máximo lucro mensal? (R: R$ 52.600,00) Segundo a professora a resposta para o máximo lucro mensal é R$ 52.600,00
é o lucro em centenas de reais. Se a produção dos termostatos está condicionada a um total de 4000 unidades por mês, quantas unidades de cada modelo a empresa deveria fabricar para obter o maior lucro possível? Qual é o máximo lucro mensal? (R: R$ 52.600,00) Segundo a professora a resposta para o máximo lucro mensal é R$ 52.600,00Vejam minhas contas:
![F(x,g,\lambda)=P(x,y)-\lambda[g(x,y)] F(x,g,\lambda)=P(x,y)-\lambda[g(x,y)]](/latexrender/pictures/18fe697a51872812b347d72206789403.png)
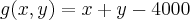
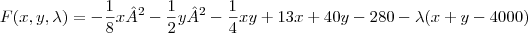
![Fx=0
[tex]Fy=0
[tex]F\lambda=0
[tex]\frac{\alpha(F)}{\alpha(x)}=0 Fx=0
[tex]Fy=0
[tex]F\lambda=0
[tex]\frac{\alpha(F)}{\alpha(x)}=0](/latexrender/pictures/f50418439b9e8f40abdf8fa26aceb49a.png)
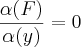
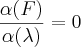
As derivadas parciais ficam assim:
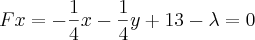
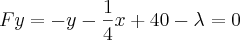
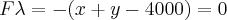
Resolvendo o sistema pra achar
 e
e  :
: 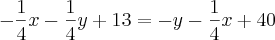
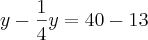
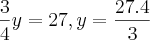
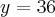
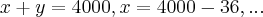
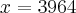
Substituindo
 e
e  na função lucro
na função lucro 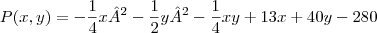
Temos:
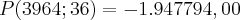
MUITO DIFERENTE DO RESULTADO ACHADO PELA PROFESSORA: R$ 52.600,00
Poderiam me ajudar em ver onde errei? Por favor?


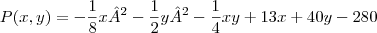
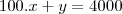

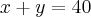
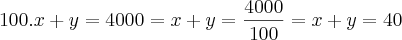
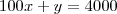
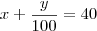
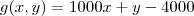

 .
.



