 por fabriel » Sáb Out 06, 2012 03:26
por fabriel » Sáb Out 06, 2012 03:26
Então, empaquei em mais uma aqui, só q ta bem complicado para mim enxergar essa substituição. E dado essa integral:
![\int_{}^{} \frac{{x}^{2}+1}{\sqrt[3]{x+1}}dx \int_{}^{} \frac{{x}^{2}+1}{\sqrt[3]{x+1}}dx](/latexrender/pictures/5fbe32bed75224b85289875b885af99f.png)
Posso escreve-la assim:

chamando:
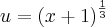
então temos que:
![du=\frac{1}{3\sqrt[3]{{u}^{2}}}dx du=\frac{1}{3\sqrt[3]{{u}^{2}}}dx](/latexrender/pictures/00d0311be8119106cbfc02d1197ecdeb.png)
Só que não consegui manipular essa expressão, de forma que substitua a outra.
Devo usar outro artifício algébrico?? quall??
Obrigado!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por MarceloFantini » Sáb Out 06, 2012 14:40
por MarceloFantini » Sáb Out 06, 2012 14:40
A substituição
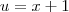
parece servir melhor, então

e assim
![\int \frac{x^2 +1}{\sqrt[3]{x+1}} \, dx = \int \frac{(u-1)^2 +1}{u^{\frac{1}{3}}} \, du = \int \frac{u^2 -2u +2}{u^{\frac{1}{3}}} \, du \int \frac{x^2 +1}{\sqrt[3]{x+1}} \, dx = \int \frac{(u-1)^2 +1}{u^{\frac{1}{3}}} \, du = \int \frac{u^2 -2u +2}{u^{\frac{1}{3}}} \, du](/latexrender/pictures/bce2eb6f82570457e9ecd995c64d5340.png)
.
Termine.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fabriel » Sáb Out 06, 2012 17:59
por fabriel » Sáb Out 06, 2012 17:59
Obrigado Marcelo!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por fabriel » Dom Nov 25, 2012 14:21
por fabriel » Dom Nov 25, 2012 14:21
Estou em duvida quanto o resultado.
Essa integral que chegamos através daquela substituição
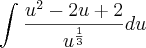
é a mais pratica??
pois ai terei que fazer um integração por partes. do tipo:

E vou chegar nisso:

Mas isso esta correto??
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por MarceloFantini » Dom Nov 25, 2012 19:17
por MarceloFantini » Dom Nov 25, 2012 19:17
Sim, é a mais prática pois
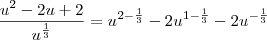
, que é simples.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fabriel » Dom Nov 25, 2012 23:49
por fabriel » Dom Nov 25, 2012 23:49
Entendo, erro meu, confundi com outra coisa aqui..
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [hora] fração de hora
 por larissagall » Ter Abr 08, 2014 17:26
por larissagall » Ter Abr 08, 2014 17:26
- 2 Respostas
- 2894 Exibições
- Última mensagem por larissagall

Qua Abr 09, 2014 09:00
Aritmética
-
- Integral por substituição / Integral por partes
por Carlos28 » Seg Out 19, 2015 12:25
- 1 Respostas
- 3038 Exibições
- Última mensagem por nakagumahissao

Seg Out 19, 2015 23:26
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição
por Aliocha Karamazov » Qui Fev 23, 2012 23:57
- 2 Respostas
- 2457 Exibições
- Última mensagem por MarceloFantini

Sex Fev 24, 2012 12:07
Cálculo: Limites, Derivadas e Integrais
-
- Integral (substituição)
por kika_sanches » Sex Mar 23, 2012 14:42
- 4 Respostas
- 3128 Exibições
- Última mensagem por kika_sanches

Sex Mar 23, 2012 15:35
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao (u.du)
por menino de ouro » Dom Nov 18, 2012 10:46
- 1 Respostas
- 1826 Exibições
- Última mensagem por young_jedi

Dom Nov 18, 2012 10:54
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{} \frac{{x}^{2}+1}{\sqrt[3]{x+1}}dx \int_{}^{} \frac{{x}^{2}+1}{\sqrt[3]{x+1}}dx](/latexrender/pictures/5fbe32bed75224b85289875b885af99f.png)

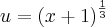
![du=\frac{1}{3\sqrt[3]{{u}^{2}}}dx du=\frac{1}{3\sqrt[3]{{u}^{2}}}dx](/latexrender/pictures/00d0311be8119106cbfc02d1197ecdeb.png)

![\int_{}^{} \frac{{x}^{2}+1}{\sqrt[3]{x+1}}dx \int_{}^{} \frac{{x}^{2}+1}{\sqrt[3]{x+1}}dx](/latexrender/pictures/5fbe32bed75224b85289875b885af99f.png)

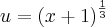
![du=\frac{1}{3\sqrt[3]{{u}^{2}}}dx du=\frac{1}{3\sqrt[3]{{u}^{2}}}dx](/latexrender/pictures/00d0311be8119106cbfc02d1197ecdeb.png)

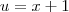 parece servir melhor, então
parece servir melhor, então  e assim
e assim![\int \frac{x^2 +1}{\sqrt[3]{x+1}} \, dx = \int \frac{(u-1)^2 +1}{u^{\frac{1}{3}}} \, du = \int \frac{u^2 -2u +2}{u^{\frac{1}{3}}} \, du \int \frac{x^2 +1}{\sqrt[3]{x+1}} \, dx = \int \frac{(u-1)^2 +1}{u^{\frac{1}{3}}} \, du = \int \frac{u^2 -2u +2}{u^{\frac{1}{3}}} \, du](/latexrender/pictures/bce2eb6f82570457e9ecd995c64d5340.png) .
.


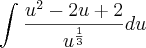 é a mais pratica??
é a mais pratica??


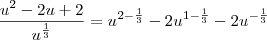 , que é simples.
, que é simples.


