 por manuel_pato1 » Sex Nov 23, 2012 01:04
por manuel_pato1 » Sex Nov 23, 2012 01:04
1 - Determinar uma equação da elipse de centro ( 0,0), eixo maior sobre o eixo dos y, sabendo que passa pelos pontos
P (1,![\sqrt[]{14} \sqrt[]{14}](/latexrender/pictures/af2c6836f15856d3c2813ea49a068a69.png) ) e Q(2,-2
) e Q(2,-2![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) )
)
Bom, tendo o eixo maior nos eixo dos y, a equação é da forma:
x²/b² + y²/a²=1
daí eu não sei tirar nada, pois pensei em substituir as coordenadas do ponto na equação , porém eu não sei a² ou b²...
resposta do livro: 2x² + y² = 16
2 - Encontrar uma equação da elipse de centro (0,0) , eixo maior sobre Ox , excentricidade 1/2 e passa pelo ponto (2,3)
Obs: Galera, realmente tentei resolver, procurar em algum lugar uma resolução pra eu entender, porém não obtive sucesso.(só pra deixar claro que não estou criando o tópico sem ao menos tentar =D)
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por young_jedi » Sex Nov 23, 2012 09:59
por young_jedi » Sex Nov 23, 2012 09:59
Fala manoel_pato1
então no primeiro substitua os pontos na equação
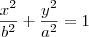
ai voce tera duas equações com a e b como incognitas resolvendo o sistema de equações voce tera a e b e com isso a equação da elipse
na dois utilizando a relação de c e a com a excentricidade e a relação de a, b e c


voce encontra b em relação a a então voce substitui na equação da elipse
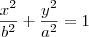
e substitui o ponto (2,3) nesta equação então voce tera uma equação em função de a, é so encontrar a e determinar b com isso voce tem a equação.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por manuel_pato1 » Sex Nov 23, 2012 13:30
por manuel_pato1 » Sex Nov 23, 2012 13:30
Opa young_jedi
cara, na primeira, eu cheguei que b²= 1/16 e a²=1/8
colocando na fórmula, ficou x²/1/16+ y²/1/8= ''?''
no ''?'' , seria 1/16 * 1/8 = 1/128 ou primeiro eu faço 16x² + 8y² = 128 ??
eu fiz do segundo modo, a resposta bateu, mas fiquei na dúvida de qual seria o valor do ''?'' , pois se eu igualasse a 128, a fórmula não voltaria a ser do fórmato anterior que é x²/1/16+ y²/1/8
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por renan_a » Sex Nov 23, 2012 14:36
por renan_a » Sex Nov 23, 2012 14:36
obrigado, também tinha dúvida
-
renan_a
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Ter Set 25, 2012 08:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por manuel_pato1 » Sex Nov 23, 2012 14:42
por manuel_pato1 » Sex Nov 23, 2012 14:42
Cara, desconsidera minha última msg. Eu estava fazendo os exercícios de elipse de uma forma errada. Eu não tirava o mmc entre a² e b² , eu tava multiplicando em X e igualava a a²*b² . O resultado batia em exercícios que a² e b² não eram multiplos, porém nesse que eu não sabia a² e b², nunca daria certo. enfim, refiz do jeito correto, e o resultado bateu. Obrigado, velho.
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (CONICAS) equação da elipse
por manuel_pato1 » Sáb Nov 17, 2012 20:53
- 4 Respostas
- 2838 Exibições
- Última mensagem por manuel_pato1

Qua Nov 21, 2012 20:44
Geometria Analítica
-
- [Cônicas] Dúvida exerc. elipse
por MrJuniorFerr » Qua Out 31, 2012 12:58
- 1 Respostas
- 1530 Exibições
- Última mensagem por young_jedi

Qua Out 31, 2012 21:00
Geometria Analítica
-
- Cônicas - Elipse - Só uma dúvida simples
por samra » Sex Jan 24, 2014 01:39
- 2 Respostas
- 1683 Exibições
- Última mensagem por samra

Sex Jan 24, 2014 19:21
Geometria Analítica
-
- Cônicas: Elipse, me ajudem, por favor!
por felipe_08 » Qui Mai 28, 2015 22:48
- 0 Respostas
- 1201 Exibições
- Última mensagem por felipe_08

Qui Mai 28, 2015 22:48
Geometria Analítica
-
- [Cônicas]Retas tangentes à cônicas
por Hopkins » Ter Fev 28, 2017 22:39
- 0 Respostas
- 1523 Exibições
- Última mensagem por Hopkins

Ter Fev 28, 2017 22:39
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{14} \sqrt[]{14}](/latexrender/pictures/af2c6836f15856d3c2813ea49a068a69.png) ) e Q(2,-2
) e Q(2,-2![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) )
)

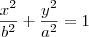




 .
.



