Oi pessoal, tava tentando resolver essa questão da PUCRS de 2007 e acabei me perdendo. Aí vai (tentativa abaixo):
Um ponto se movimenta sobre um plano onde está situado
um referencial cartesiano. Seu trajeto percorre a
circunferência de equação x² + y² = 1 e seu deslocamento
é feito a partir do ponto ( 1, 0 ) no sentido antihorário
até a primeira interseção dessa circunferência
com a reta y = x. Essa interseção é dada pelo ponto
A) (cos0º, sen0º)
B) (sen30º, cos 30º)
C) (cos 45º, sen 45º)
D) (sen 60º, cos60º)
E) (sen90º, cos90º)
O que eu fiz foi o seguinte: desenhei a o círculo com centro (0,0) e raio 1 e a reta y=x. Marquei o ponto 1,0 e fiz a trajetória, até chegar no ponto de interseção, que para mim ficou no segundo quadrante. Agora não sei o que fazer! Como descubro as coordenadas do ponto?
Obrigado!


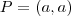 simultaneamente pertencente a circunferência e a reta , como
simultaneamente pertencente a circunferência e a reta , como  estar no segundo quadrante ,
estar no segundo quadrante ,  . Assim ,
. Assim , 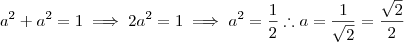 . Mas ,
. Mas ,  daí ,
daí , 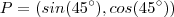 .
.
 denota uma reta que faz um ângulo de
denota uma reta que faz um ângulo de 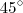 com o eixo x, portanto este será o ângulo. Como o raio é um, podemos descrever o ponto como
com o eixo x, portanto este será o ângulo. Como o raio é um, podemos descrever o ponto como  .
. ,
, 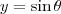 e faça
e faça  .
.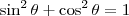 , logo
, logo 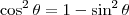 .
.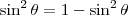 ,
, 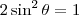 e
e 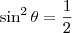 .
. ou
ou  .
. ou
ou 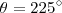 . Como queremos a primeira interseção, a resposta é
. Como queremos a primeira interseção, a resposta é 

