por cabooze » Qui Nov 22, 2012 13:38
por cabooze » Qui Nov 22, 2012 13:38
Este é meu primeiro post:
Estou procurando a equação da variação da área de fechamento de uma válvula esférica em função do tempo.
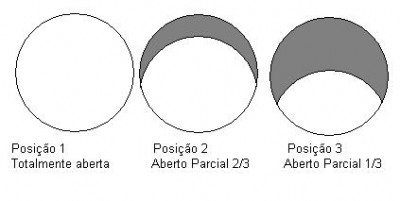
- Ilustração de fechamento
*Imagem ilustrativa
Não consigo montar a equação da área de fechamento em função do tempo para calcular a área de fechamento.
Por exemplo:
Na figura a posição 1, a área fechada é 0 cm e a área aberta é de 4

cm²
Na posição 2, a parte cinza corresponde a área fechada.
O problema é calcular a área já fechada e o que me falta é a função pela variação do tempo.
O tempo médio para fechar completamente a válvula é de

T=221ms.
Como faço para encontrar essa função?
Começando Iniciação Cientifica!
-

cabooze
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 22, 2012 12:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Quimica
- Andamento: cursando
 por cabooze » Ter Nov 27, 2012 10:09
por cabooze » Ter Nov 27, 2012 10:09
Ninguem pode dar uma ajuda ou uma dica?
Começando Iniciação Cientifica!
-

cabooze
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 22, 2012 12:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Quimica
- Andamento: cursando
 por young_jedi » Ter Nov 27, 2012 12:20
por young_jedi » Ter Nov 27, 2012 12:20
meu amigo,
um sugestão que eu daria seria determinar um eixo x em que a tampa se desloca neste eixo
dai voce teria que utilizar calculo integral para calcular a area coberta
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Taxa de variacao - area do circulo !
por andersoneng » Sex Jun 29, 2012 10:40
- 2 Respostas
- 2920 Exibições
- Última mensagem por Russman

Sex Jun 29, 2012 21:18
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas Parcias (Diferenciais): tx de variação área/vol
por jpreis » Sáb Jul 13, 2013 15:36
- 2 Respostas
- 2719 Exibições
- Última mensagem por jpreis

Sáb Jul 13, 2013 18:44
Cálculo: Limites, Derivadas e Integrais
-
- Determinar tempo de aplicacao
por radg » Seg Mai 17, 2010 16:14
- 0 Respostas
- 1349 Exibições
- Última mensagem por radg

Seg Mai 17, 2010 16:14
Matemática Financeira
-
- Juros composto Tempo?
por djeffersound » Qua Jun 23, 2010 19:45
- 0 Respostas
- 2840 Exibições
- Última mensagem por djeffersound

Qua Jun 23, 2010 19:45
Matemática Financeira
-
- Lógica - Unidade de tempo
por ViniRFB » Sex Fev 15, 2013 01:12
- 2 Respostas
- 1837 Exibições
- Última mensagem por ViniRFB

Sex Fev 15, 2013 01:16
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 cm²
cm² T=221ms.
T=221ms.