


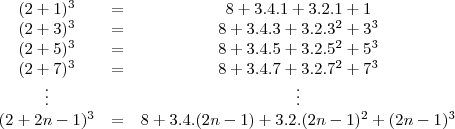

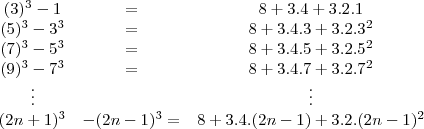
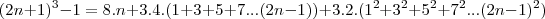



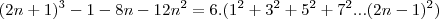
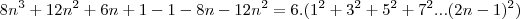
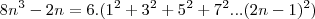
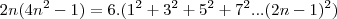
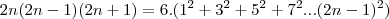





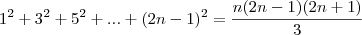

young_jedi escreveu:é na ultima equação voce passa o 3 dividindo para o outro lado da expressão e ai voce chega justamente na relação que voce queria demonstrar.



MarceloFantini escreveu:Apesar de ser uma solução, ela não é por indução.




MarceloFantini escreveu:Antes que eu me esqueça, não crie tópicos repetidos. Eu joguei o outro na lixeira.
Resolvi comentar que a solução não é por indução porque, apesar de não ter sido explícito no enunciado, você nomeou o tópico como Indução Matemática. Assim presumi que a idéia é resolver por indução. Você sabe quais são os passos para provar uma afirmação por indução?

rbhorvath escreveu:Então estamos aprendendo indução matemática porém no enunciado o professor não especificou o método que deveria ser resolvido portanto acho que não tem importância como é resolvido e sim o resultado...
Não sei como resolver esse exercício por indução matemática
 .
. .
.



Cleyson007 escreveu:Olá, bom dia a todos!
Resolvendo por indução:
Vamos provar que a igualdade é válida para n = 1---> 1² = 1(2 - 1)(2 + 1)/3 <---> 1=1 (OK)
Vamos supor que seja válida para n = k ---> 1² + 3² + ... + (2k - 1)² = k(2k - 1)(2k + 1)/3
Logo, também será válida para n = k+1. Acompanhe:
1² + 3² + ... + (2k - 1)² + (2k + 1)² = k(2k - 1)(2k + 1)/3 + 4k² + 4k + 1 = (4n³ + 12n² + 11n + 3)/3 = (k + 1)(2(k + 1) - 1)(2(k + 1) + 1)/3
Comente qualquer dúvida
Att,
Cleyson007



Cleyson007 escreveu:Olá rbhorvath!
Sim, está correto
Abraço,
Cleyson007




Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes