 com um
com um  resultado no que chamamos de soma; a subtração, em diferença; a multiplicação, em produto; a divisão em razão; a radiciação em raiz; e a potenciação em: "..." ?
resultado no que chamamos de soma; a subtração, em diferença; a multiplicação, em produto; a divisão em razão; a radiciação em raiz; e a potenciação em: "..." ?Percebi que existem dois sinais para a multiplicação e para a divisão:
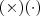 e
e 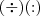 , respectivamente. Dizem ser a mesma coisa, mas estou achando que os sinais de
, respectivamente. Dizem ser a mesma coisa, mas estou achando que os sinais de 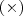 e de
e de 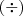 são para os fatores enquanto que
são para os fatores enquanto que  e
e 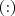 são para os coeficentes e para os expoentes. Neste contexto, penso que há uma enorme diferença entre coeficiente e fator:
são para os coeficentes e para os expoentes. Neste contexto, penso que há uma enorme diferença entre coeficiente e fator: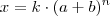 => (a+b):=parcelas; k:=coeficiente; n:=expoente
=> (a+b):=parcelas; k:=coeficiente; n:=expoente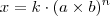 => (a×b):=fatores; k:=coeficiente; n:=expoente
=> (a×b):=fatores; k:=coeficiente; n:=expoenteMinhas deduções procedem?
Outra dúvida é com relação à divisão: a divisão entre segmentros, entre áreas ou entre volumes resulta num valor abstrato, denominado de razão, isso eu compreendo. O que eu não entendo intuitivamente bem é a operação de dividir uma área por um segmento de reta, ou a de dividir um volume por uma área ou por um segmento de reta. Gostaria de compreender isso melhor.
Obg!




 como uma parcela em
como uma parcela em 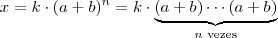 . Como disse, não há diferença no termo mesmo que seja
. Como disse, não há diferença no termo mesmo que seja  ao invés de
ao invés de 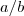 para multiplicação e divisão. Quase ninguém escreve
para multiplicação e divisão. Quase ninguém escreve 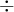 ou
ou 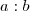 . Nos livros mais modernos pelo menos esta notação é abandonada completamente.
. Nos livros mais modernos pelo menos esta notação é abandonada completamente.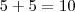 (10 é chamado de soma);
(10 é chamado de soma); (15 é o produto);
(15 é o produto); (25 é um
(25 é um 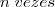 " ! É "
" ! É "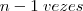 " .
" . parcelas/fatores, o que é verdade.
parcelas/fatores, o que é verdade.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.