 por Jhenrique » Sáb Nov 10, 2012 19:48
por Jhenrique » Sáb Nov 10, 2012 19:48
Para começar: a adição de um elemento

com um

resultado no que chamamos de
soma; a subtração, em
diferença; a multiplicação, em
produto; a divisão em
razão; a radiciação em
raiz; e a potenciação em:
"..." ?
Percebi que existem dois sinais para a multiplicação e para a divisão:
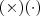
e
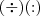
, respectivamente. Dizem ser a mesma coisa, mas estou achando que os sinais de
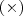
e de
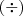
são para os fatores enquanto que

e
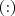
são para os coeficentes e para os expoentes. Neste contexto, penso que há uma enorme diferença entre coeficiente e fator:
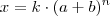
=> (a+b):=parcelas; k:=coeficiente; n:=expoente
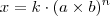
=> (a×b):=fatores; k:=coeficiente; n:=expoente
Minhas deduções procedem?
Outra dúvida é com relação à divisão: a divisão entre segmentros, entre áreas ou entre volumes resulta num valor abstrato, denominado de
razão, isso eu compreendo. O que eu não entendo intuitivamente bem é a operação de dividir uma área por um segmento de reta, ou a de dividir um volume por uma área ou por um segmento de reta. Gostaria de compreender isso melhor.
Obg!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sáb Nov 10, 2012 22:19
por MarceloFantini » Sáb Nov 10, 2012 22:19
Jhenrique escreveu:Para começar: a adição de um elemento

com um

resultado no que chamamos de
soma; a subtração, em
diferença; a multiplicação, em
produto; a divisão em
razão; a radiciação em
raiz; e a potenciação em:
"..." ?
Potenciação em potência?
Jhenrique escreveu:Percebi que existem dois sinais para a multiplicação e para a divisão:
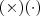
e
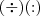
, respectivamente. Dizem ser a mesma coisa, mas estou achando que os sinais de
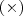
e de
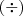
são para os fatores enquanto que

e
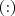
são para os coeficentes e para os expoentes. Neste contexto, penso que há uma enorme diferença entre coeficiente e fator:
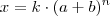
=> (a+b):=parcelas; k:=coeficiente; n:=expoente
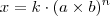
=> (a×b):=fatores; k:=coeficiente; n:=expoente
Minhas deduções procedem?
Não procedem. Parcelas ou fatores são a mesma coisa, não há diferença entre estes termos.
Jhenrique escreveu:Outra dúvida é com relação à divisão: a divisão entre segmentros, entre áreas ou entre volumes resulta num valor abstrato, denominado de razão, isso eu compreendo. O que eu não entendo intuitivamente bem é a operação de dividir uma área por um segmento de reta, ou a de dividir um volume por uma área ou por um segmento de reta. Gostaria de compreender isso melhor.
Obg!
A divisão entre números resulta em um número. Por que insiste em fazer correspondências físicas absurdas desprovidas de quaisquer bases científicas? Parece que também não leu
minha resposta ao seu último tópico. Por favor, faça-o. Você tem insistido num assunto que está claramente errado e não tem perspectivas de parar, apesar de todos os argumentos e evidências contrários. Se continuar assim, pararei de responder.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Sáb Nov 10, 2012 22:49
por Jhenrique » Sáb Nov 10, 2012 22:49
MarceloFantini escreveu:Potenciação em potência?
Humm... mas potência não é o mesmo que expoente?
MarceloFantini escreveu:Minhas deduções procedem?
Não procedem. Parcelas ou fatores são a mesma coisa, não há diferença entre estes termos.
Acho que onde vc escreveu "parcelas", tinha em mente "coeficiente", ok!
MarceloFantini escreveu:A divisão entre números resulta em um número. Por que insiste em fazer correspondências físicas absurdas desprovidas de quaisquer bases científicas? Parece que também não leu
minha resposta ao seu último tópico. Por favor, faça-o. Você tem insistido num assunto que está claramente errado e não tem perspectivas de parar, apesar de todos os argumentos e evidências contrários. Se continuar assim, pararei de responder.
Você checkou a hora que eu abri estes tópicos? Eu ia abrir 1 só, mas achei que ia ficar mto volumoso, então abri 2.
Como assim ñ tem base científica? E as contruções geométricas em geometria plana? E a geometria descritiva? Nestes campos, eu nem preciso necessariamente definir uma unidade física, basta eu marcar 2 pontos e dizer que a distancia entre eles é a minha unidade para as contruções, sem física e sem nada! Só para ilustrar, multiplicando um segmento

por um

o resultado é área formada entre esses segmentos em condição perpendicular e interseccionados nos extermos.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Sáb Nov 10, 2012 23:59
por MarceloFantini » Sáb Nov 10, 2012 23:59
Jhenrique escreveu:MarceloFantini escreveu:Potenciação em potência?
Humm... mas potência não é o mesmo que expoente?
Sim, mas costumamos falar "segunda potência" ao invés de "segundo expoente", então parece ser uma boa designação.
Jhenrique escreveu:MarceloFantini escreveu:Não procedem. Parcelas ou fatores são a mesma coisa, não há diferença entre estes termos.
Acho que onde vc escreveu "parcelas", tinha em mente "coeficiente", ok!
Não, quis dizer parcelas mesmo. Você se referiu a

como uma parcela em
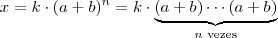
. Como disse, não há diferença no termo mesmo que seja

ao invés de

. Esqueci de comentar na outra resposta, mas vai agora: a notação mais comum ainda é

e
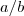
para multiplicação e divisão. Quase ninguém escreve
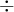
ou
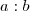
. Nos livros mais modernos pelo menos esta notação é abandonada completamente.
Jhenrique escreveu:Como assim ñ tem base científica? E as contruções geométricas em geometria plana? E a geometria descritiva? Nestes campos, eu nem preciso necessariamente definir uma unidade física, basta eu marcar 2 pontos e dizer que a distancia entre eles é a minha unidade para as contruções, sem física e sem nada! Só para ilustrar, multiplicando um segmento

por um

o resultado é área formada entre esses segmentos em condição perpendicular e interseccionados nos extermos.
Sim, é adotada como unidade no sentido de que tem magnitude unitária (pela própria palavra). Se não me engano, definimos a área de um retângulo como sendo o produto dos lados e deduzimos as demais áreas das figuras geométricas a partir desta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Jhenrique » Dom Nov 11, 2012 02:51
por Jhenrique » Dom Nov 11, 2012 02:51
Exemplificando minha 1ª pergunta:
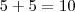
(10 é chamado de soma);

(15 é o produto);

(25 é um
anônimo)
MarceloFantini escreveu:Não, quis dizer parcelas mesmo. Você se referiu a

como uma parcela em
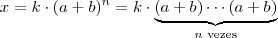
Marcelo, não é "
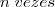
" ! É "
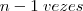
" .
No curso de técnico e de engenharia mecânica, quando dimensionamos uma viga, p ex, adicionamos à fórmula um valor que uns chamam de coeficiente de segurança e outros de fator de segurança (ou coeficiente de cagaço! kkkk). Daí eu fiquei pensando, "o correto é coeficiente ou fator?" Bem... essa ñ deve ser uma pergunta de matemática e sim de latim. Já eliminaram o latim das escolas, se deus quiser elimam a matemática também.
MarceloFantini escreveu:Sim, é adotada como unidade no sentido de que tem magnitude unitária (pela própria palavra). Se não me engano, definimos a área de um retângulo como sendo o produto dos lados e deduzimos as demais áreas das figuras geométricas a partir desta.
Acho que o espírito da minha pergunta ficou claro agora. Fornecer 3 segmentos de retas e solicitar a construção do volume é simples, queria é entender como ficaria a construção entre o produto de dois segmentos divido por um terceiro.
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por MarceloFantini » Dom Nov 11, 2012 04:21
por MarceloFantini » Dom Nov 11, 2012 04:21
Jhenrique escreveu:Exemplificando minha 1ª pergunta:
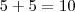
(10 é chamado de soma);

(15 é o produto);

(25 é um
anônimo)
Seria 5 à segunda potência.
Jhenrique escreveu:MarceloFantini escreveu:Não, quis dizer parcelas mesmo. Você se referiu a

como uma parcela em
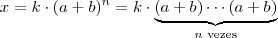
Marcelo, não é "
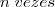
" ! É "
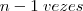
" .
Você está correto. Eu quis dizer

parcelas/fatores, o que é verdade.
Jhenrique escreveu:No curso de técnico e de engenharia mecânica, quando dimensionamos uma viga, p ex, adicionamos à fórmula um valor que uns chamam de coeficiente de segurança e outros de fator de segurança (ou coeficiente de cagaço! kkkk). Daí eu fiquei pensando, "o correto é coeficiente ou fator?" Bem... essa ñ deve ser uma pergunta de matemática e sim de latim. Já eliminaram o latim das escolas, se deus quiser elimam a matemática também.
Engenheiros em geral não se importam com nomenclatura ou tomar cuidado para que a terminologia esteja correta.
Jhenrique escreveu:MarceloFantini escreveu:Sim, é adotada como unidade no sentido de que tem magnitude unitária (pela própria palavra). Se não me engano, definimos a área de um retângulo como sendo o produto dos lados e deduzimos as demais áreas das figuras geométricas a partir desta.
Acho que o espírito da minha pergunta ficou claro agora. Fornecer 3 segmentos de retas e solicitar a construção do volume é simples, queria é entender como ficaria a construção entre o produto de dois segmentos divido por um terceiro.
Não sei responder à esta sua pergunta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 com um
com um  resultado no que chamamos de soma; a subtração, em diferença; a multiplicação, em produto; a divisão em razão; a radiciação em raiz; e a potenciação em: "..." ?
resultado no que chamamos de soma; a subtração, em diferença; a multiplicação, em produto; a divisão em razão; a radiciação em raiz; e a potenciação em: "..." ?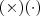 e
e 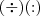 , respectivamente. Dizem ser a mesma coisa, mas estou achando que os sinais de
, respectivamente. Dizem ser a mesma coisa, mas estou achando que os sinais de 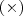 e de
e de 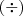 são para os fatores enquanto que
são para os fatores enquanto que  e
e 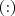 são para os coeficentes e para os expoentes. Neste contexto, penso que há uma enorme diferença entre coeficiente e fator:
são para os coeficentes e para os expoentes. Neste contexto, penso que há uma enorme diferença entre coeficiente e fator: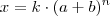 => (a+b):=parcelas; k:=coeficiente; n:=expoente
=> (a+b):=parcelas; k:=coeficiente; n:=expoente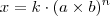 => (a×b):=fatores; k:=coeficiente; n:=expoente
=> (a×b):=fatores; k:=coeficiente; n:=expoente



 como uma parcela em
como uma parcela em 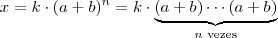 . Como disse, não há diferença no termo mesmo que seja
. Como disse, não há diferença no termo mesmo que seja  ao invés de
ao invés de 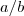 para multiplicação e divisão. Quase ninguém escreve
para multiplicação e divisão. Quase ninguém escreve 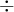 ou
ou 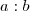 . Nos livros mais modernos pelo menos esta notação é abandonada completamente.
. Nos livros mais modernos pelo menos esta notação é abandonada completamente.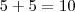 (10 é chamado de soma);
(10 é chamado de soma); (15 é o produto);
(15 é o produto); (25 é um
(25 é um 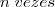 " ! É "
" ! É "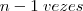 " .
" . parcelas/fatores, o que é verdade.
parcelas/fatores, o que é verdade.