
eu começei assim : chamei u de :
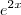 entao du =
entao du = 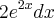 chamei dv : cos( x )dx então v = sen(x)
chamei dv : cos( x )dx então v = sen(x)utilizando a formula da integral por partes (u)(dv):

encontrei:
 agora eu tenho que resolver a nova integral? correto? para que? ainda não sei direito o porque?
agora eu tenho que resolver a nova integral? correto? para que? ainda não sei direito o porque?como continua esse exercicio ? eu sei que a resposta tem que dar :
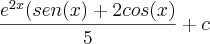
nao sei como chegar até aqui ,gostaria de aprender como que se resolve de uma maneira mais facil de entender! obrigado


 . Quando você resolver esta nova integral você voltará à integral original. A partir disso, você substitui a primitiva que encontrar, que terá a integral original, e resolva para encontrar a primitiva. Se não ficar muito claro, poste os novos cálculos que discutiremos passo a passo.
. Quando você resolver esta nova integral você voltará à integral original. A partir disso, você substitui a primitiva que encontrar, que terá a integral original, e resolva para encontrar a primitiva. Se não ficar muito claro, poste os novos cálculos que discutiremos passo a passo.

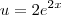


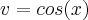

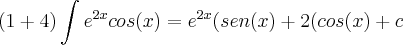
 ,
,  ,
, implica em
implica em  , pois na verdade é
, pois na verdade é  . Devido ao sinal de menos na integral anterior eles cancelaram-se e você chegou na resposta certa, mas tome cuidado da próxima vez. No mais, está tudo correto.
. Devido ao sinal de menos na integral anterior eles cancelaram-se e você chegou na resposta certa, mas tome cuidado da próxima vez. No mais, está tudo correto.