 por thejotta » Seg Out 29, 2012 13:06
por thejotta » Seg Out 29, 2012 13:06
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por thejotta » Seg Out 29, 2012 17:03
por thejotta » Seg Out 29, 2012 17:03
Muito obrigado amigo...
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por thejotta » Seg Out 29, 2012 19:13
por thejotta » Seg Out 29, 2012 19:13
amigos mais uma duvida como posso determina a solução do sistema usando o processo de eliminação gaussianae usando o sistema de gauss-jordan???
fico grato desde já pela ajuda.
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Seg Out 29, 2012 19:32
por e8group » Seg Out 29, 2012 19:32
thejotta , você tem que aplicar as
operações elementares na matriz aumentada .
Recomendo a leitura do assunto
aqui !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por thejotta » Seg Out 29, 2012 22:21
por thejotta » Seg Out 29, 2012 22:21
caro amigo santhiago eu tentei fazer mais não estou conseguindo me diga aonde esta o erro comecei assim:
solucionar o sistema com eliminação gaussiana

matriz aumentada
depois cheguei a essa matriz
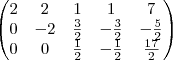
chegando a esse sistema

não sei se esta certo e se estiver como resolver
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por thejotta » Ter Out 30, 2012 09:28
por thejotta » Ter Out 30, 2012 09:28
alguém ????
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Ter Out 30, 2012 12:02
por e8group » Ter Out 30, 2012 12:02
thejotta , mesmo se vc estar certo , o processo não facilitou uma solução para o sistema linear .
Segue as seguintes etapas com as operações elementares na matriz aumentada .
Eliminação 1 :

Eliminação 2 :

Eliminação 3 :
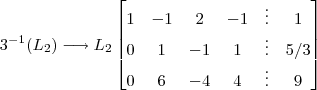
Eliminação 4 :
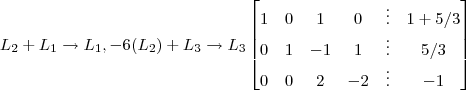
Eliminação 5 :
![2^{-1}[L_3] \rightarrow L_3 \begin{bmatrix} 1 & 0 & 1 & 0 & \vdots & 1 + 5/3 \\ 0 & 1 & -1 & 1 & \vdots & 5/3 \\ 0& 0 & 1 & -1 & \vdots & -1/2 \end{bmatrix} 2^{-1}[L_3] \rightarrow L_3 \begin{bmatrix} 1 & 0 & 1 & 0 & \vdots & 1 + 5/3 \\ 0 & 1 & -1 & 1 & \vdots & 5/3 \\ 0& 0 & 1 & -1 & \vdots & -1/2 \end{bmatrix}](/latexrender/pictures/abc8b6a85992caa6d3c65bfea6cb1fa1.png)
Eliminação 6 :
tente concluir ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- obter o sistema linear de temperatura e obter na forma AX=B
por netochaves » Sáb Abr 06, 2013 18:20
- 0 Respostas
- 2360 Exibições
- Última mensagem por netochaves

Sáb Abr 06, 2013 18:20
Álgebra Linear
-
- obter o sistema linear de temperatura e obter na forma AX=B
por netochaves » Dom Abr 21, 2013 19:22
- 0 Respostas
- 1942 Exibições
- Última mensagem por netochaves

Dom Abr 21, 2013 19:22
Álgebra Linear
-
- [Representação Matricial] Op. linear definido por rotação
por 12200633 » Dom Jun 01, 2014 19:17
- 1 Respostas
- 2408 Exibições
- Última mensagem por ant_dii

Seg Jun 02, 2014 05:28
Álgebra Linear
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3080 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- Transformação Linear - Forma de realizar cálculo
por talesalberto » Seg Nov 03, 2014 21:49
- 1 Respostas
- 1433 Exibições
- Última mensagem por Russman

Ter Nov 04, 2014 01:38
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


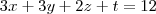



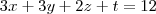





 matriz aumentada
matriz aumentada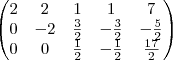





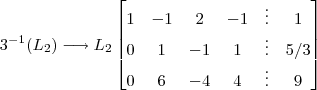
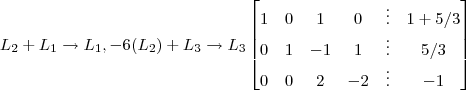
![2^{-1}[L_3] \rightarrow L_3 \begin{bmatrix} 1 & 0 & 1 & 0 & \vdots & 1 + 5/3 \\ 0 & 1 & -1 & 1 & \vdots & 5/3 \\ 0& 0 & 1 & -1 & \vdots & -1/2 \end{bmatrix} 2^{-1}[L_3] \rightarrow L_3 \begin{bmatrix} 1 & 0 & 1 & 0 & \vdots & 1 + 5/3 \\ 0 & 1 & -1 & 1 & \vdots & 5/3 \\ 0& 0 & 1 & -1 & \vdots & -1/2 \end{bmatrix}](/latexrender/pictures/abc8b6a85992caa6d3c65bfea6cb1fa1.png)
