 por thejotta » Seg Out 29, 2012 13:06
por thejotta » Seg Out 29, 2012 13:06
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por thejotta » Seg Out 29, 2012 17:03
por thejotta » Seg Out 29, 2012 17:03
Muito obrigado amigo...
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por thejotta » Seg Out 29, 2012 19:13
por thejotta » Seg Out 29, 2012 19:13
amigos mais uma duvida como posso determina a solução do sistema usando o processo de eliminação gaussianae usando o sistema de gauss-jordan???
fico grato desde já pela ajuda.
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Seg Out 29, 2012 19:32
por e8group » Seg Out 29, 2012 19:32
thejotta , você tem que aplicar as
operações elementares na matriz aumentada .
Recomendo a leitura do assunto
aqui !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por thejotta » Seg Out 29, 2012 22:21
por thejotta » Seg Out 29, 2012 22:21
caro amigo santhiago eu tentei fazer mais não estou conseguindo me diga aonde esta o erro comecei assim:
solucionar o sistema com eliminação gaussiana

matriz aumentada
depois cheguei a essa matriz
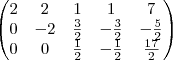
chegando a esse sistema

não sei se esta certo e se estiver como resolver
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por thejotta » Ter Out 30, 2012 09:28
por thejotta » Ter Out 30, 2012 09:28
alguém ????
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Ter Out 30, 2012 12:02
por e8group » Ter Out 30, 2012 12:02
thejotta , mesmo se vc estar certo , o processo não facilitou uma solução para o sistema linear .
Segue as seguintes etapas com as operações elementares na matriz aumentada .
Eliminação 1 :

Eliminação 2 :

Eliminação 3 :
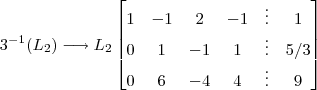
Eliminação 4 :
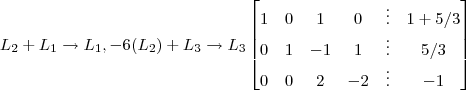
Eliminação 5 :
![2^{-1}[L_3] \rightarrow L_3 \begin{bmatrix} 1 & 0 & 1 & 0 & \vdots & 1 + 5/3 \\ 0 & 1 & -1 & 1 & \vdots & 5/3 \\ 0& 0 & 1 & -1 & \vdots & -1/2 \end{bmatrix} 2^{-1}[L_3] \rightarrow L_3 \begin{bmatrix} 1 & 0 & 1 & 0 & \vdots & 1 + 5/3 \\ 0 & 1 & -1 & 1 & \vdots & 5/3 \\ 0& 0 & 1 & -1 & \vdots & -1/2 \end{bmatrix}](/latexrender/pictures/abc8b6a85992caa6d3c65bfea6cb1fa1.png)
Eliminação 6 :
tente concluir ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- obter o sistema linear de temperatura e obter na forma AX=B
por netochaves » Sáb Abr 06, 2013 18:20
- 0 Respostas
- 2360 Exibições
- Última mensagem por netochaves

Sáb Abr 06, 2013 18:20
Álgebra Linear
-
- obter o sistema linear de temperatura e obter na forma AX=B
por netochaves » Dom Abr 21, 2013 19:22
- 0 Respostas
- 1943 Exibições
- Última mensagem por netochaves

Dom Abr 21, 2013 19:22
Álgebra Linear
-
- [Representação Matricial] Op. linear definido por rotação
por 12200633 » Dom Jun 01, 2014 19:17
- 1 Respostas
- 2408 Exibições
- Última mensagem por ant_dii

Seg Jun 02, 2014 05:28
Álgebra Linear
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3083 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- Transformação Linear - Forma de realizar cálculo
por talesalberto » Seg Nov 03, 2014 21:49
- 1 Respostas
- 1434 Exibições
- Última mensagem por Russman

Ter Nov 04, 2014 01:38
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


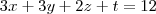



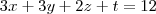





 matriz aumentada
matriz aumentada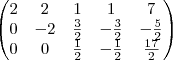





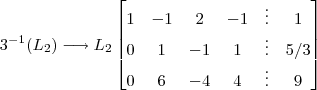
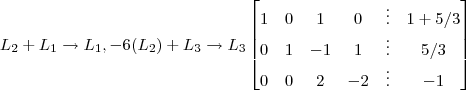
![2^{-1}[L_3] \rightarrow L_3 \begin{bmatrix} 1 & 0 & 1 & 0 & \vdots & 1 + 5/3 \\ 0 & 1 & -1 & 1 & \vdots & 5/3 \\ 0& 0 & 1 & -1 & \vdots & -1/2 \end{bmatrix} 2^{-1}[L_3] \rightarrow L_3 \begin{bmatrix} 1 & 0 & 1 & 0 & \vdots & 1 + 5/3 \\ 0 & 1 & -1 & 1 & \vdots & 5/3 \\ 0& 0 & 1 & -1 & \vdots & -1/2 \end{bmatrix}](/latexrender/pictures/abc8b6a85992caa6d3c65bfea6cb1fa1.png)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
