 por MrJuniorFerr » Sáb Out 27, 2012 20:02
por MrJuniorFerr » Sáb Out 27, 2012 20:02
Estou com dúvida no seguinte exercício:
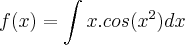
Estou com uma certa dificuldade nas integrais trigonométricas neste conteúdo, o resto consigo fazer.
Tentei fazer este, mas não deu certo...
Eu havia feito a seguinte substituição:
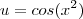
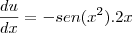
Após montar a substituição, fiz isto:

Depois disto, ao tentar fazer, cheguei no resultado:
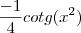
Mas sei que está errado pois,
![\frac{d[\frac{-1}{4}cotg(x^2)]}{dx} = \frac{d[\frac{-1}{4}cotg(x^2)]}{dx} =](/latexrender/pictures/71e085c07a7b1481d77ce9ac8b885618.png)

Alguém pode me ajudar?
Outra pergunta: Só pode jogar constantes para fora da integral?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por young_jedi » Sáb Out 27, 2012 20:17
por young_jedi » Sáb Out 27, 2012 20:17
neste caso uma melhor substituição seria
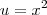

substituindo na integral


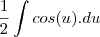
esta integral é mais tranquila
respondendo sua pergunta, voce so pode tirar da integral constantes, não pode tirar termos que dependam da variavel de integração neste caso x.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MrJuniorFerr » Sáb Out 27, 2012 21:49
por MrJuniorFerr » Sáb Out 27, 2012 21:49
Entendi Jedi.
Mas se a integral fosse:
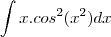
Como resolve-lo?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por young_jedi » Sáb Out 27, 2012 22:54
por young_jedi » Sáb Out 27, 2012 22:54
eu faria a mesma substituição, entãoa integral ficaria

mais note que
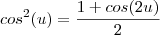
então a intgral ficaria

esta integral da para resolver por antiderivada
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MrJuniorFerr » Sáb Out 27, 2012 23:33
por MrJuniorFerr » Sáb Out 27, 2012 23:33
young_jedi escreveu:mais note que
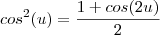
identidade trigonométrica?
Em derivadas, era possível esquivar-se das identidades trigonométricas porque os exercícios pediam somente que derivassem e não necessariamente simplificar ao máximo.
Em integrais é obrigatório simplificar ao máximo?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Dom Out 28, 2012 00:26
por MarceloFantini » Dom Out 28, 2012 00:26
Lembre-se das identidades

e

. Some as duas e isole

que você obterá a identidade afirmada.
Sobre simplificações, elas valem para o geral: em princípio, após todas as contas que você fizer deve-se simplificar ao máximo a resposta. O caso é que muitas vezes em derivadas, principalmente nas mais simples, a resposta já sai simplificado, o que não necessariamente é verdade em integração.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Dom Out 28, 2012 01:25
por MrJuniorFerr » Dom Out 28, 2012 01:25
Entendi, fiz o que você disse e cheguei em tal identidade. Eu não conhecia este método de somar identidades e isolar algum termo para obter uma nova identidade

Tive um ensino fundamental e médio horrível, eu não estudava nem em véspera de provas, ou seja, entrei em uma universidade federal (por sorte) com uma base horrível em exatas, e to pagando o preço agora...
Ao menos abri meus olhos, talvez um pouco tarde, mas abri.
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Regra da cadeia para derivadas parciais
por Maisa_Rany » Qua Nov 07, 2018 16:47
- 2 Respostas
- 9474 Exibições
- Última mensagem por Maisa_Rany

Qui Nov 08, 2018 16:33
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo II - Regra da Cadeia para várias variáveis
por Guga1981 » Qua Nov 11, 2020 02:22
- 3 Respostas
- 4442 Exibições
- Última mensagem por Guga1981

Dom Nov 22, 2020 05:02
Cálculo: Limites, Derivadas e Integrais
-
- [ regra da cadeia ]
por Marimar » Seg Nov 07, 2011 13:34
- 3 Respostas
- 3061 Exibições
- Última mensagem por MarceloFantini

Seg Nov 07, 2011 14:37
Cálculo: Limites, Derivadas e Integrais
-
- Regra da Cadeia
por Cleyson007 » Ter Mai 22, 2012 15:17
- 1 Respostas
- 1889 Exibições
- Última mensagem por joaofonseca

Ter Mai 22, 2012 19:14
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas- regra da cadeia
por genicleide » Qua Abr 20, 2011 14:28
- 4 Respostas
- 4949 Exibições
- Última mensagem por genicleide

Qua Abr 20, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
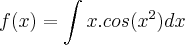
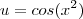
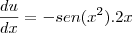

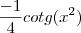
![\frac{d[\frac{-1}{4}cotg(x^2)]}{dx} = \frac{d[\frac{-1}{4}cotg(x^2)]}{dx} =](/latexrender/pictures/71e085c07a7b1481d77ce9ac8b885618.png)



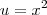



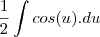
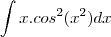

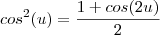

 e
e  . Some as duas e isole
. Some as duas e isole  que você obterá a identidade afirmada.
que você obterá a identidade afirmada.




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.