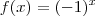 ela pode ser interpretada visualmente assim
ela pode ser interpretada visualmente assim  , ou seja, eu sei explicitamente o que acontece se o x variar, porque a parte real é
, ou seja, eu sei explicitamente o que acontece se o x variar, porque a parte real é  e a parte imaginária é
e a parte imaginária é 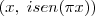 .
.Agora, se uma função polinomial do 2º grau chamada
 , por exemplo, gera um número complexo
, por exemplo, gera um número complexo 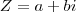 eu não sei o que isso significa. Eu não sei o que acontece caso eu variar o
eu não sei o que isso significa. Eu não sei o que acontece caso eu variar o  ... não sei se o termo
... não sei se o termo  varia na mesma proporção.. e somar
varia na mesma proporção.. e somar  tem algum significado... o que acontece se eu variar o
tem algum significado... o que acontece se eu variar o  , o
, o  varia na mesma proporção, ou o
varia na mesma proporção, ou o  ou nenhum dos dois??????
ou nenhum dos dois??????Não consigo fazer essas experiências empíricas no GeoGebra. MUITO do que eu aprendi sobre função foi graças ao GeoGebra. Mas ele não é um bom programa para funções complexas. Então não consigo compreendê-las.
PS: Abri um tópico na seção Numeros Complexos intitulado [Z=a+bi] Entendendo isso melhor para tratar extamente dessa dúvida e manter o fórum organizado.


 ? Porque sabendo do formato padrão da função exponencial, dado uma lista de pontos no plano xy, eu também poderia descobrir a expressão que intersecta esses pontos!
? Porque sabendo do formato padrão da função exponencial, dado uma lista de pontos no plano xy, eu também poderia descobrir a expressão que intersecta esses pontos! 
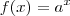 , com
, com  e
e 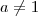 . A função que escreveu pode ser obtida por operações com outras funções, como composições e produtos.
. A função que escreveu pode ser obtida por operações com outras funções, como composições e produtos.





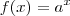 ).
).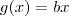 e
e 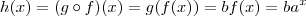 , ou mesmo
, ou mesmo  e
e 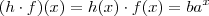 .
. . Novamente, perceba que pode ser obtida por operações com as funções
. Novamente, perceba que pode ser obtida por operações com as funções  ,
, 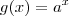 ,
,  ,
, 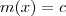 . Faça
. Faça  .
. é uma função característica duma PA de 1ª ordem e
é uma função característica duma PA de 1ª ordem e 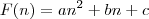 duma de 2ª.
duma de 2ª. ?
? ,
,  e assim em diante? Mostre suas contas, elas não fazem sentido para mim. Qual o propósito de integrar uma função exponencial? Onde está a sequência e a relação encontrada a partir dela, como disse? Além do mais, a definição algébrica é posterior aos cálculos aritméticos.
e assim em diante? Mostre suas contas, elas não fazem sentido para mim. Qual o propósito de integrar uma função exponencial? Onde está a sequência e a relação encontrada a partir dela, como disse? Além do mais, a definição algébrica é posterior aos cálculos aritméticos.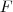 da função
da função 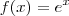 é
é 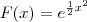 . Basta aplica o limite abaixo na função primitiva e o resultado será a sua derivada.
. Basta aplica o limite abaixo na função primitiva e o resultado será a sua derivada.![\lim_{h->0} \sqrt[h]{\frac{f(x+h)}{f(x)}} \lim_{h->0} \sqrt[h]{\frac{f(x+h)}{f(x)}}](/latexrender/pictures/773323a5adaddee9b66b2f8819194e95.png)
 é
é  .
.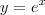 tem coeficiente angular constante, ou seja, é uma reta.
tem coeficiente angular constante, ou seja, é uma reta.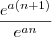 e o resultado será
e o resultado será  . O coeficiente
. O coeficiente  , o que você está fazendo é impossível. Não existe continuidade em conjuntos como os naturais ou os inteiros.
, o que você está fazendo é impossível. Não existe continuidade em conjuntos como os naturais ou os inteiros.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.